
 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
 解:
解: ;当x=4时,y=4
;当x=4时,y=4 )(1分)
)(1分)

 x+1(4分)
x+1(4分) ,则四边FOMG和四边形NOMH均为矩形,设FO=x(3分)
,则四边FOMG和四边形NOMH均为矩形,设FO=x(3分)
 (4分)
(4分) (6分)
(6分)
 ,AC=
,AC=

 ∴
∴ (10分)
(10分) x2)(x>0),
x2)(x>0), x2,OM=x
x2,OM=x (11分)
(11分)
 =2(13分)
=2(13分) =2
=2

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:2009年福建省莆田市中考数学试卷(解析版) 题型:解答题
 x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF.
x2上的两点A、B的横坐标分别为-1和4,直线AB交y轴于点F,过点A、B分别作直线l的垂线,垂足分别为点C、D,连接CF、DF. x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
x2对称轴右侧图象上的一动点,过点P作PQ⊥PO交x轴于点Q,是否存在点P使得△OPQ与△CDF相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《三角形》(12)(解析版) 题型:解答题
 a;
a; a;结论2. AD+BE+CF=
a;结论2. AD+BE+CF= a;
a;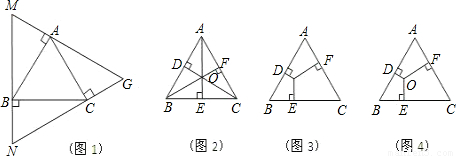
查看答案和解析>>
科目:初中数学 来源:2010年云南省楚雄州双柏县中考数学模拟试卷(妥甸中学)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2009-2010学年江苏省扬州市梅岭中学九年级(下)期中数学试卷(解析版) 题型:解答题
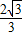 ,求⊙O的半径r.
,求⊙O的半径r.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com