
【题目】如图,将![]() 绕着点B顺时针旋转至
绕着点B顺时针旋转至![]() ,使得C点落在AB的延长线上的D点处,
,使得C点落在AB的延长线上的D点处,![]() 的边BC恰好是
的边BC恰好是![]() 的角平分线.
的角平分线.
(1)试求旋转角![]() 的度数;
的度数;
(2)设BE与AC的交点为点P,求证:![]() .
.

【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据旋转的性质,得到∠ABC=EBD,由BC平分∠EBD,得到∠ABE=∠EBC=∠CBD,根据平角定义,即可得到答案;
(2)由(1)知,∠EBC=∠CBD=60°,由三角形外角定理可得,![]() 则
则![]() 即可得到结论成立.
即可得到结论成立.
(1)解:由旋转的性质,得:∠ABC=∠EBD,
即![]() ,
,
∴∠ABE=∠CBD,
∵BC平分∠EBD,
∴∠EBC=∠CBD,
∴∠ABE=∠EBC=∠CBD,
∵∠ABE+∠EBC+∠CBD=180°,
∴∠CBD=60°.
(2)证明:如图,BE与AC相交与点P,DE与AC相交与点F,

由(1)知,∠EBC=∠CBD=60°,
由三角形外角定理,得:∠APB=∠EBC+∠C=60°+∠C,∠CBD=∠A+∠C=60°,
∴∠APB=∠A+2∠C
∴∠APB>∠A,结论成立.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
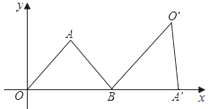
【题目】如图,△AOB为等腰三角形,顶点A的坐标(2,![]() ),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
),底边OB在x轴上.将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B,点A的对应点A′在x轴上,则点O′的坐标为( )
A. (![]() ,
,![]() ) B. (
) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,4
,4![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平行四边形ABCD中,BF平分![]() 交AD于点F,AE
交AD于点F,AE![]() BF于点O,交BC于点E,连接EF.
BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形;
(2)若AE=6,BF=8,CE=3,求四边形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.
(1)求证:①△ABE≌△ACF;②△AEF是等边三角形;
(2)①当点E运动到什么位置时,EF⊥DC?
②若AB=4,当∠EAB=15°时,求△CEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
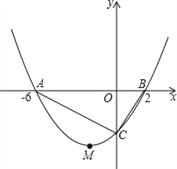
【题目】如图,抛物线y=ax2+bx+c的顶点为M(﹣2,﹣4),与x轴交于A、B两点,且A(﹣6,0),与y轴交于点C.
(1)求抛物线的函数解析式;
(2)求△ABC的面积;
(3)能否在抛物线第三象限的图象上找到一点P,使△APC的面积最大?若能,请求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件中,最适合使用全面调查的方式收集数据的是( )
A.了解某地区人民对修建高速路的意见
B.了解同批次![]() 灯泡的使用寿命
灯泡的使用寿命
C.了解我校七年级某班同学的课外阅读时间
D.了解昆明市中学生对“社会主义核心价值观”的知晓率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 轴于点
轴于点![]() ,且三角形
,且三角形![]() 的面积是
的面积是![]() .
.
(![]() )求点
)求点![]() ,
,![]() 的坐标;
的坐标;
(![]() )点
)点![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的两个动点,点
上的两个动点,点![]() 从点
从点![]() 向左以
向左以![]() 个单位长度/秒运动,同时点
个单位长度/秒运动,同时点![]() 从点
从点![]() 向点
向点![]() 以
以![]() 个单位长度/秒运动,如图所示,设运动时间为
个单位长度/秒运动,如图所示,设运动时间为![]() 秒
秒![]() .
.
①当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
②是否存在一段时间,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某餐厅中,一张桌子可坐6人,有如图所示的两种摆放方式:

(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌.若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N为山两侧的两个村庄,为了两村交通方便,根据国家的惠民政策,政府决定打一直线涵洞,工程人员为计算工程量,必须测量M、N两点之间的直线距离.选择测量点A、B、C,点B、C分别在AM、AN上,现测得AM=1千米,AN=1.8千米,AB=54米,BC=45米,AC=30米,求M、N两点之间的直线距离.

【答案】M、N两点之间的直线距离为1500米.
【解析】试题分析:先根据相似三角形的判定得出△ABC∽△AMN,再利用相似三角形的性质解答即可.
试题解析:在△ABC与△AMN中, ![]() ,
, ![]() =
=![]() ,∴
,∴![]() ,又∵∠A=∠A,
,又∵∠A=∠A,
∴△ABC∽△AMN,∴![]() ,即
,即![]() ,
,
解得:MN=1500米,
答:M、N两点之间的直线距离是1500米;
考点:相似三角形的应用.
【题型】解答题
【结束】
23
【题目】如图,在△ADC中,点B是边DC上的一点,∠DAB=∠C, ![]() .若△ADC的面积为18cm,求△ABC的面积.
.若△ADC的面积为18cm,求△ABC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com