
����Ŀ��ijѧУΪ��չ����������������ƻ��ó�������3000Ԫ���ʽ���һ��������ë���ĺ�ƹ�����ģ���֪������ë���ĺ�ƹ�����ĵĵ��۱�Ϊ8:3��2�����䵥�ۺ�Ϊ130Ԫ��
��1������������ë���ĺ�ƹ�����ĵĵ��۷ֱ��Ƕ���Ԫ��
��2����Ҫ����������ë���ĺ�ƹ�����ĵ���������80������������ë���ĵ�������ƹ������������4�����ҹ���ƹ�����ĵ�����������15�������м��ֹ��������ַ���������ʹ�˷����٣������˷��Ƕ��٣�
���𰸡���1��������ë���ĺ�ƹ�����ĵĵ��۷ֱ�Ϊ80Ԫ��30Ԫ��20Ԫ����2��һ������������������һ�������٣������˷���2900Ԫ.
��������
��1���赥�۱��е�ÿһ��Ϊx����ʾ���䵥�ۣ����ݵ��ۺͿ����x�����������Ӧ���ۼ��ɣ�
��2����ϵʽΪ��ƹ�����ĵ�������15���ܼۡ�3000���������ֵ������ú��ʵ�������ĸ������ɣ�
��1����������ë���ĺ�ƹ�����ĵĵ��۱�Ϊ8�U3�U2��
�����������ǵĵ��۷ֱ�Ϊ8x��3x��2xԪ��
�����⣬��8x+3x+2x=130�����x=10��
��������ë���ĺ�ƹ�����ĵĵ��۷ֱ�Ϊ80Ԫ��30Ԫ��20Ԫ��
��2���蹺�����������Ϊy����
������ë���ĵ�����Ϊ4y��������ƹ�����ĵ�����Ϊ��80-y-4y������
�������⣬��![]()
���13��y��14��
��yȡ������
��yֻ��ȡ13��14��
��ˣ�һ��������������
����һ����y=13ʱ��������13������ë���Ĺ���52����ƹ�����Ĺ���15����
����������y=14ʱ��������14������ë���Ĺ���56����ƹ�����Ĺ���10����
����һ�������٣�Ϊ2900Ԫ.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ,��
,��![]() �ֱ���
�ֱ���![]() ֱ���ϣ���
ֱ���ϣ���![]() Ϊ��ƽ�����ڲ�һ��
Ϊ��ƽ�����ڲ�һ��

��1����ͼ1��![]() ��ƽ���߽��ڵ�N����
��ƽ���߽��ڵ�N����![]() ����
����![]() ����
����![]() �Ķ���
�Ķ���
��2����ͼ2����GΪֱ��![]() ��һ�㣬��
��һ�㣬��![]() ���ӳ�GM��ֱ��AB�ڵ�Q����PΪMG��һ�㣬����
���ӳ�GM��ֱ��AB�ڵ�Q����PΪMG��һ�㣬����![]() �ཻ�ڵ�H������
�ཻ�ڵ�H������![]() ����
����![]() ����
����![]() �Ķ�������
�Ķ�������![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��ͼ����ͼ��ʾ���������ĸ����ۣ���a+b+c��0����a+c=b����b=��2a����4ac��b2��0��������ȷ�Ľ����У� �� 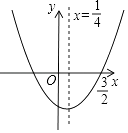
A.4��
B.3��
C.2��
D.1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �ס�������ѧ���ڲμӽ�����������ǰ������5��������Զ���ԣ����˵�ƽ���ɼ���ͬ�����м�����óɼ��ķ�����0.005��������õijɼ����£�2.20 m,2.30 m,2.30 m,2.40 m,2.30 m,��ô�ס��ҵijɼ��Ƚϣ� ��
A.�ijɼ����ȶ�B.�ҵijɼ����ȶ�
C.�ס��ҵijɼ�һ���ȶ�D.����ȷ��˭�ijɼ����ȶ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֽƬABCD����ͼ��ʾ�ķ�ʽ�۵���AE��EFΪ�ۺۣ���BAE=30�㣬AB= ![]() ���۵���C����AD���ϵ�C1�������ҵ�B����EC1���ϵ�B1������BC�ij�Ϊ�� ��
���۵���C����AD���ϵ�C1�������ҵ�B����EC1���ϵ�B1������BC�ij�Ϊ�� �� 
A.![]()
B.2
C.3
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������ͨ�У�ij�㳡�ƻ����½�Ϊ30�㣬�³�Ϊ60��б��AB���и��죬��б���е�D����ȥ�������壨��Ӱ��ʾ������һ��ƽ����ˮƽ��CA��ƽ̨DE��һ���µ�б��BE��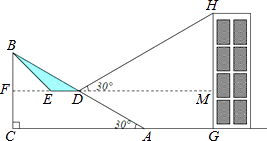
��1��������б��BE���½�Ϊ36�㣬��ƽ̨DE�ij�ԼΪ�����ף�
��2���ھ����½�A��27��Զ��G�����̳���¥��С����D������¥����H ������Ϊ30�㣬��ô��¥GH��ԼΪ�����ף������ȡ�������ο����ݣ�sin36��=0.6��cos36��=0.8��tan36��=0.7�� ![]() =1.7��
=1.7��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ�ǡ�ABC�ƶ���B��ת����ͼλ�ã����С�C=90�㣬AB=4��BC=2����C��B��A����ͬһֱ���ϣ�����Ӱ���ֵ������ �� 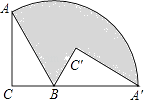
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������18�֣�ijУ�ˣ�1����ͬѧΪ�˽�2011��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ�������������
�¾���ˮ�� | Ƶ�������� | Ƶ�� |
| 6 | 0��12 |
| 0��24 | |
| 16 | 0��32 |
| 10 | 0��20 |
| 4 | |
| 2 | 0��04 |
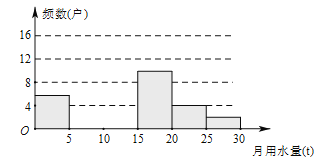
�����������⣺
��1���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2������С����ˮ��������15t�ļ�ͥռ�������ͥ�����İٷֱȣ�
��3������С����1000����ͥ�����ݵ������ݹ��ƣ���С���¾���ˮ������20 t�ļ�ͥ��Լ�ж��ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��1.25x2+4.25x+1��y�ύ��A�㣬����A��ֱ���������߽�����һ��B������B��BC��x�ᣬ����Ϊ��C��3��0��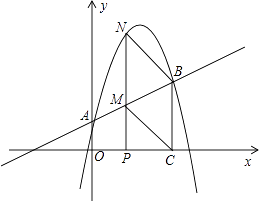
��1����ֱ��AB�ĺ�����ϵʽ��
��2������P���߶�OC�ϴ�ԭ�������ÿ��һ����λ���ٶ���C�ƶ�������P��PN��x�ᣬ��ֱ��AB�ڵ�M�����������ڵ�N�����P�ƶ���ʱ��Ϊt�룬MN�ij���Ϊs����λ����s��t�ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��3�����ڣ�2���������£������ǵ�P���O����C�غϵ������������CM��BN����tΪ��ֵʱ���ı���BCMNΪƽ���ı��Σ��ʶ��������tֵ��ƽ���ı���BCMN�Ƿ����Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com