
【题目】(1)如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.
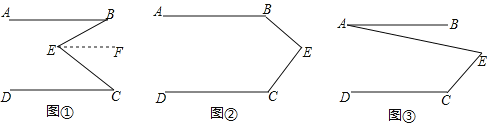
证明过程如下:
证明:过点E作EF∥AB,
∵AB∥DC,EF∥AB(辅助线的作法),
∴EF∥DC
∴∠C=∠CEF.
∵EF∥AB,∴∠B=∠BEF
∴∠B+∠C=∠CEF+∠BEF
即∠B+∠C=∠BEC.
(2)如果点E运动到图②所示的位置,其他条件不变,∠B,∠C,∠BEC又有什么关系?并证明你的结论;
(3)如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A= .(写出结论,不用写计算过程)。
【答案】(2)∠B+∠C=360°﹣∠BEC;证明见解析;(3)20°.
【解析】(1)(2)(3)分别过E作EF∥AB,根据平行线的判定得出AB∥CD∥EF,根据平行线的性质得出即可.
(2)证明:如图②,过点E作EF∥AB,
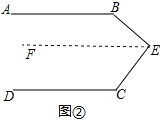
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠B+∠BEF=180°,
∴∠B+∠C+∠AEC=360°,
∴∠B+∠C=360°﹣∠BEC;
(3)解:如图③,过点E作EF∥AB,
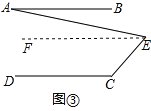
∵AB∥DC(已知),EF∥AB(辅助线的作法),
∴EF∥DC(平行于同一直线的两直线平行),
∴∠C+∠CEF=180°,∠A=∠BEF,
∵∠C=120°,∠AEC=80°,
∴∠CEF=180°﹣120°=60°,
∴∠BEF=80°﹣60°=20°,
∴∠A=∠BEF=20°.
故答案为:20°.
“点睛”本题考查了平行线的性质和判定的应用,能正确作出辅助线是解题的关键,注意:(1)两直线平行,内错角相等;(2)两直线平行,同位角相等;(3)两直线平行,同旁内角互补,以及平行于同一直线的两直线平行的运用.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】用一根长为24 cm的铁丝围成一个长与宽的比是2∶1的长方形,则长方形的面积是( ).
A. 32 cm2 B. 36 cm2 C. 144 cm2 D. 以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 处于中间位置的数为这组数据的中位数
B. 中间两个数的平均数为这组数据的中位数
C. 要想了解一批电磁炉的使用寿命,适合采用全面调查的方法
D. 公司员工月收入的众数为3500元.说明该公司中月收入3500元的员工最多
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】半径为R的⊙O中,弦AB=2R,弦CD=R,若两弦的弦心距分别为OE、OF,则OE∶OF等于( )
A. 2∶1 B. 3∶2 C. 2∶3 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com