
����Ŀ��ʦ������Ϊ�����������ڵ�֪����������������������ص�һ�����ɹ����ó����������������ֹ�ɹ�3�˾�ס��С���۸�ÿ��160Ԫ���ɹ�10�˾�ס�Ĵ����۸�ÿ��400Ԫ��ѧУ��ȥ���96000Ԫ�ɹ������ÿɹ�2300����ʱ��ס��
��1�����У�ɹ��˶��ٶ�3��С���������ٶ�10�˴�����
��2��ѧУ�ƻ����üס��������ͺŵĿ�����20�����������������������������֪���Ϳ���ÿ����ͬʱװ��4��С�����11�����������Ϳ���ÿ����ͬʱװ��12��С�����7����������ΰ��żס������ֿ�������һ���Խ����������������������ļ��ַ�����
���𰸡���:��1����ѧУ�ɹ���x��С����y�������������⣬��![]()
�ⷽ�����![]() ����ѧУ�ɹ���100��3��С����200��10�˴�����
����ѧУ�ɹ���100��3��С����200��10�˴�����
��2������Ϳ�������a������ô���Ϳ������ţ�20-a ���������������
![]() ���15
���15![]() ��Ϊ������ ������������a =15��16��17������20- a =5��4��3���ʰ��ŷ��������֣������Ϳ���15�������Ϳ���5����
��Ϊ������ ������������a =15��16��17������20- a =5��4��3���ʰ��ŷ��������֣������Ϳ���15�������Ϳ���5����
�����Ϳ���16�������Ϳ���4������ ���Ϳ���17�������Ϳ���3����
�������������������1��������ɹ���x��3��С����y��10�˴������г���Ԫһ�η����飮
��2������Ϳ���������a���������Ϳ��������ˣ�20��a�������г�����ʽ���ɣ�
�⣺��1����ɹ���x��3��С����y��10�˴�����
��������![]() ��
��
���![]() ��
��
�𣺲ɹ���100��3��С����200��10�˴�����
��2������Ϳ���������a���������Ϳ��������ˣ�20��a��������
![]() ��
��
���15��a��17.5
��a������
��a=15��16��17
�����Ϳ�����20��a=5��4��3
����3�ַ�����
�����Ϳ���15�������Ϳ���5����
�����Ϳ���16�������Ϳ���4����
�����Ϳ���17�������Ϳ���3����


 ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д�
ѧ�ڸ�ϰһ��ͨѧϰ�ܶ�Ա��ĩ������ӱ����������ϵ�д� â���̸����������������ϵ�д�
â���̸����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y1=a��x-m��2+k��y2=a��x+m��2+k��m��0������y��Գƣ����dz�y1��y2��Ϊ����г�����ߡ�����д��������y=-4x2+6x+7�ġ���г�����ߡ� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ѿ���ֽƬABCD��EF�۵���ʹ��B���ڱ�AD�ϵĵ�B��������A���ڵ�A������
��1����֤��B��E=BF��
��2����AE=a��AB=b��BF=C���Բ���a��b��c֮���һ�ֹ�ϵ��������֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��2��AC��![]() ����BAC��105������ABD����ACE����BCF���ǵȱ������Σ����ı���AEFD�����Ϊ__________
����BAC��105������ABD����ACE����BCF���ǵȱ������Σ����ı���AEFD�����Ϊ__________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�ڣ�һ���������Ϊ��2����3������������x��ԳƵĵ�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����й涨����Ʊÿ����ǡ�������������10%����������ԭ�۵�10%�㲻�����ǣ�������ͣ��������ԭ�۵�10%�㲻���ٵ���������ͣ����һ֧��Ʊij���ͣ��֮������ʱ�����ǻص�ԭ�ۣ���������˹�Ʊ�ɼ۵�ƽ��������Ϊx����x����ķ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ֱ��
��ֱ��![]() ����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
����A��B���㣬��x����D��C���㣬����AC��BC����֪A��0��3����C��3��0����
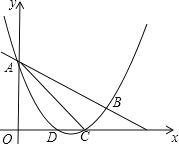
�������������ߵĽ���ʽ��tan��BAC��ֵ��
�������ڣ����������£�
��1��PΪy���Ҳ���������һ���㣬����PA������P��PQ��PA��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ���������������ACB���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
��2����EΪ�߶�AC��һ�㣨�����˵㣩������DE��һ����M�ӵ�D���������߶�DE��ÿ��һ����λ�ٶ��˶���E�㣬�����߶�EA��ÿ��![]() ����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�(ֱ��д���𰸣�
����λ���ٶ��˶���A��ֹͣ������E�������Ƕ���ʱ����M�������˶�����ʱ���٣�(ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���� A B C��![]() ��ƽ��ֱ������ϵ�е�λ����ͼ.
��ƽ��ֱ������ϵ�е�λ����ͼ.
��1���ֱ�д�����и�������꣺ ![]() ______ ��
______ �� ![]() _______ ��
_______ �� ![]() _______ ��
_______ ��
��2��˵��![]() ���� A B C����������ƽ�Ƶõ�����________________________________��
���� A B C����������ƽ�Ƶõ�����________________________________��
��3������![]() ��
��![]() ��
�� ![]() ������ A B C�ڲ�һ�㣬��ƽ�ƺ�
������ A B C�ڲ�һ�㣬��ƽ�ƺ�![]() �ڵĶ�Ӧ��
�ڵĶ�Ӧ��![]() ������Ϊ ________ ��
������Ϊ ________ ��
��4������ A B C�����..
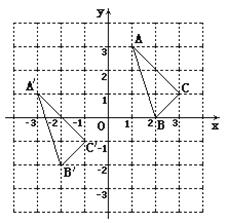
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʱ���У�ʱ�������֮��ļн�Ϊ300���ǣ���
A. �糿6�� B. ����13�� C. ����12�� D. ����9��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com