
分析 (1)根据两种优惠方案列式子即可;
(2)将x=10代入,分别计算即可;
(3)哪种方案花费少,那么这种方案就合理.
解答 解:(1)按方案①购买花费:5x+60(元);
按方案②购买花费:4.5x+72(元);
故答案为:5x+60;4.5x+72;
(2)当x=10时,5x+60=50+60=110,
4.5x+72=45+72=117,
故答案为:110;117;
(3)运用方案①购买4个书包,得到免费4支水性笔,
再运用方案②购买8支水性笔,
这样共用去80+8×5×0.9=116(元).
点评 本题考查了列代数式以及代数式求值的知识,解答本题的关键是仔细审题,得出两种方案下需要的花费.


科目:初中数学 来源: 题型:解答题
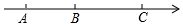 已知数轴上有A,B,C三点,它们分别表示数a,b,c,且|a+24|+|b+10|=0,又b,c互为相反数.
已知数轴上有A,B,C三点,它们分别表示数a,b,c,且|a+24|+|b+10|=0,又b,c互为相反数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
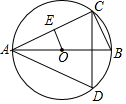 如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°
如图,已知AB是⊙O的直径,点C,D在⊙O上,且AB=6,∠CAB=30°查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com