
分析 (1)直接配上一次项系数的一半的平方,再进一步利用非负数的性质证明即可;
(2)先两前面两项提-9得到-9x2+8x-2=-9(x2-$\frac{8}{9}$x)-2,再利用配方法得到-9x2+8x-2=-9(x-$\frac{4}{9}$)2-$\frac{2}{9}$,然后根据非负数的性质进行证明.
解答 (1)证明:a2-a+1
=a2-a+$\frac{1}{4}$-$\frac{1}{4}$+1
=(a-$\frac{1}{2}$)2+$\frac{3}{4}$
∵(a-$\frac{1}{2}$)2≥0
∴(a-$\frac{1}{2}$)2+$\frac{3}{4}$>0
即a2-a+1的值为正;
(2)证明:-9x2+8x-2=-9(x2-$\frac{8}{9}$x)-2
=-9(x2-$\frac{8}{9}$x+$\frac{16}{81}$-$\frac{16}{81}$)-2
=-9(x-$\frac{4}{9}$)2-$\frac{2}{9}$
∵9(x-$\frac{4}{9}$)2≥0,
∴-9(x-$\frac{4}{9}$)2≤0,
∴-9(x-$\frac{4}{9}$)2-$\frac{2}{9}$<0,
即-9x2+8x-2<0
点评 此题考查配方法的运用,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
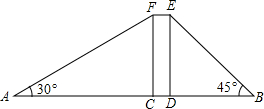 宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:
宾哥和君哥在华润广场前感慨楼房真高.君哥说:“这楼起码20层!”宾哥不以为然:“20层?我看没有,数数就知道了!”君哥说:“老大,不有办法不用数就知道吗?”宾哥想了想说:“没问题!让我们量一量把!”君哥、宾哥在楼体两侧各选A、B两点,其中CDEF表示楼体,AB=200米,CD=20米.∠A=30°,∠B=45°,(A、C、D、E四点在同一直线上)问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
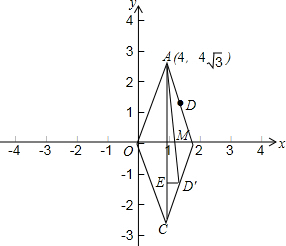 如图,直角坐标系中,四边形ABCO是菱形,对角线OB在x轴正半轴上,点A的坐标为(4,4$\sqrt{3}$),点D为AB的中点.动点M从点O出发沿x轴向点B运动,运动的速度为每秒1个单位,试解答下列问题:
如图,直角坐标系中,四边形ABCO是菱形,对角线OB在x轴正半轴上,点A的坐标为(4,4$\sqrt{3}$),点D为AB的中点.动点M从点O出发沿x轴向点B运动,运动的速度为每秒1个单位,试解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).
平面直角坐标系上点A(1,4),点B(5,2),点C(2,1),若x轴上有一点D,使点A和点B到直线CD的距离相等,那么满足条件的点D的坐标是(4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com