
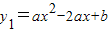 的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB=2OC=3.
的顶点为D,与x轴交于点A,B,与y轴交于点C,且OB=2OC=3.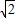 DQ,试求出y2关于x的函数关系式;
DQ,试求出y2关于x的函数关系式; 分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为
分别与抛物线y1交于点E,G,与y2的函数图象交于点F,H.问点E、F、H、G围成四边形的面积能否为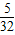 ?若能,求出m的值;若不能,请说明理由.
?若能,求出m的值;若不能,请说明理由.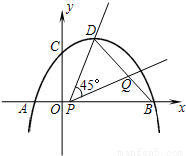
 )两点,利用待定系数法求得二次函数解析式中的未知数的值即可确定其解析式;
)两点,利用待定系数法求得二次函数解析式中的未知数的值即可确定其解析式;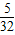 ,从假设出发求得m的值就说明存在,否则就不存在.
,从假设出发求得m的值就说明存在,否则就不存在.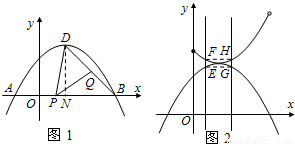 解:(1)∵OB=2,OC=
解:(1)∵OB=2,OC= ,
, )两点,
)两点,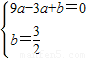 ,
,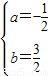
 x2+x+
x2+x+ .
. x2+x+
x2+x+ 易得D(1,2),N(1,0),A(-1,0),B(3,0),
易得D(1,2),N(1,0),A(-1,0),B(3,0),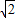 ,
,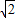 )2-22=PD2-(1-x)2①
)2-22=PD2-(1-x)2①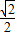 y2×2
y2×2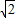 ②.
②. x2-x+
x2-x+ .
. x2-x+
x2-x+ =
= (x-1)2+2(0≤x<3).
(x-1)2+2(0≤x<3).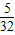 (如图2)
(如图2) x2+x+
x2+x+ =-
=- (x-1)2+2(分别与直线x=m,x=m+
(x-1)2+2(分别与直线x=m,x=m+ 的交点
的交点 (m-1)2+2),G(m+
(m-1)2+2),G(m+ ,-
,- (m-1)2+2).
(m-1)2+2). (m-1)2+2),H(m+
(m-1)2+2),H(m+ ,-
,- (m-
(m- )2+2).
)2+2). (m-1)2+2-[-
(m-1)2+2-[- (m-1)2+2]=(m-1)2
(m-1)2+2]=(m-1)2 (m-
(m- )2+2-[-
)2+2-[- (m-
(m- )2+2]=(m-
)2+2]=(m- )2.
)2. [(m-1)2+(m-
[(m-1)2+(m- )2]×
)2]× =
=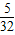
 或
或 (都在0≤x≤3内)
(都在0≤x≤3内) 或
或 时,E、F、H、G围成四边形的面积为
时,E、F、H、G围成四边形的面积为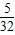 .
.

科目:初中数学 来源: 题型:
| 1 | 2 |
 点.
点.查看答案和解析>>
科目:初中数学 来源: 题型:
 21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).
21、如图,抛物线的顶点为A(1,-4),且过点B(3,0).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为
(2013•河南)如图,抛物线的顶点为P(-2,2),与y轴交于点A(0,3).若平移该抛物线使其顶点P沿直线移动到点P′(2,-2),点A的对应点为A′,则抛物线上PA段扫过的区域(阴影部分)的面积为查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(2013•峨眉山市二模)已知,如图,抛物线的顶点为C(1,-2),直线y=kx+m与抛物线交于A、B两点,其中OA=3,B点在y轴上.点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
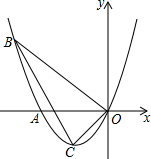 (2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.
(2013•鄂尔多斯)如图,抛物线的顶点为C(-1,-1),且经过点A、点B和坐标原点O,点B的横坐标为-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com