
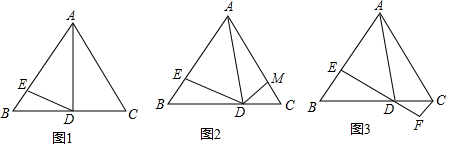
分析 (1)根据等边三角形的性质得到∠BAD=30°,∠ADB=90°,根据直角三角形的性质得到BD=$\frac{1}{2}AB$,BE=$\frac{1}{2}$BD=$\frac{1}{4}$AB,于是得到AE=3BE;
(2)由于△ABC是等边三角形,得到∠B=∠C=60°,推出∠1=∠2根据相似三角形的性质得到CM•AB=BE•AC,由于AB=AC,于是得到CM=BE;
(3)根据相似三角形的性质即可得到结论.
解答 解:(1)∵△ABC为等边三角形,点D是BC的中点,
∴∠BAD=30°,∠ADB=90°,
∴BD=$\frac{1}{2}AB$,
∵∠ADE=60°,
∴∠AED=90°,
∴∠DEB=90°,∠BDE=30°,
∴BE=$\frac{1}{2}$BD=$\frac{1}{4}$AB,
∴AE=3BE;
(2)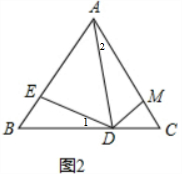 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴∠B=∠C=60°,
∵∠EDA=60°,
∴∠1+∠ADC=120°,
∵∠2+∠ADC=120°,
∴∠1=∠2,
∴△BED∽△CDA,
∴$\frac{BE}{CB}=\frac{BD}{AC}$,即BE•AC=BD•CD,
同理△DCM∽△ABD,∴$\frac{CM}{BD}=\frac{DC}{AB}$,即CM•AB=BD•DC,
∴CM•AB=BE•AC,
∵AB=AC,
∴CM=BE;
(3)FC+BE=DC,由(2)得,△ADC∽△DEB,
∵CF∥BA,
∴△ADC∽△DFC,
∴$\frac{FC}{DC}=\frac{DC}{AC}$,$\frac{BE}{DC}=\frac{DB}{AC}$,
∴$\frac{FC+BE}{DC}=\frac{DC+DB}{AC}$,
∴$\frac{FC+BE}{DC}=\frac{CB}{AC}=1$,
∴FC+BE=DC.
点评 本题考查了等边三角形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:填空题
| x | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
| x2-x-1.1 | -0.71 | -0.54 | -0.35 | -0.14 | 0.09 | 0.34 | 0.61 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
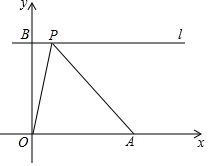 如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.
如图,在平面直角坐标系中,点A的坐标为(5,0),点B的坐标为(0,4),过点B作直线l平行x轴,点P在直线l上运动.设点P的横坐标为a,记点B关于直线OP的对称点为B′,若点B′落在△OAP内部(不包括边上),则a的取值范围为2<a<4.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图①,在直角梯形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y.若y关于x的函数图象如图②所示,则△BCD的面积是3.
如图①,在直角梯形ABCD中,动点P从点B出发,沿BC、CD运动至点D停止,设点P运动的路程为x,△ABP的面积为y.若y关于x的函数图象如图②所示,则△BCD的面积是3.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com