
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形,其中一定成立的是( )| A. | ①② | B. | ③④ | C. | ②③ | D. | ①③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道.若设人行道的宽度为x米,则可以列出关于x的方程是( )| A. | x2+9x-8=0 | B. | x2-9x-8=0 | C. | x2-9x+8=0 | D. | 2x2-9x+8=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
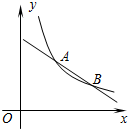 如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1).
如图,反比例函数y=$\frac{k}{x}$(x>0)与一次函数y=ax+b的图象交于点A(m,m+1)、B(m+3,m-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com