
【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2 . 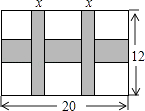
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的 ![]() ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.
【答案】
(1)解:根据题意可知,横彩条的宽度为 ![]() xcm,
xcm,
∴  ,
,
解得:0<x<8,
y=20× ![]() x+2×12x﹣2×
x+2×12x﹣2× ![]() xx=﹣3x2+54x,
xx=﹣3x2+54x,
即y与x之间的函数关系式为y=﹣3x2+54x(0<x<8)
(2)解:根据题意,得:﹣3x2+54x= ![]() ×20×12,
×20×12,
整理,得:x2﹣18x+32=0,
解得:x1=2,x2=16(舍),
∴ ![]() x=3,
x=3,
答:横彩条的宽度为3cm,竖彩条的宽度为2cm
【解析】(1)由横、竖彩条的宽度比为3:2知横彩条的宽度为 ![]() xcm,根据:三条彩条面积=横彩条面积+2条竖彩条面积﹣横竖彩条重叠矩形的面积,可列函数关系式;(2)根据:三条彩条所占面积是图案面积的
xcm,根据:三条彩条面积=横彩条面积+2条竖彩条面积﹣横竖彩条重叠矩形的面积,可列函数关系式;(2)根据:三条彩条所占面积是图案面积的 ![]() ,可列出关于x的一元二次方程,整理后求解可得.
,可列出关于x的一元二次方程,整理后求解可得.


科目:初中数学 来源: 题型:
【题目】为迎接“六一”儿童节的到来,某校学生参加献爱心捐款活动,随机抽取该校部分学生的捐款数进行统计分析,相应数据的统计图如下: 
(1)该样本的容量是 , 样本中捐款15元的学生有人;
(2)若该校一共有500名学生,据此样本估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程kx2﹣4x+2=0有实数根.
(1)求k的取值范围;
(2)若△ABC中,AB=AC=2,AB,BC的长是方程kx2﹣4x+2=0的两根,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
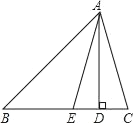
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
(1)若∠B=38°,∠C=70°,求∠DAE的度数;
(2)若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,抛物线y=ax2+bx(a<0)的图象与x轴交于A、O两点,顶点为B,将该抛物线的图象绕原点O旋转180°后,与x轴交于点C,顶点为D,若此时四边形ABCD恰好为矩形,则b的值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前20天每天的价格y1(元/件)与时间t(天)的函数关系式为:y1= ![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣
t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围. 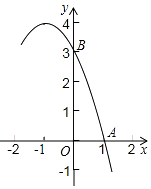
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是 ![]() 的中点,CE⊥AB于E,BD交CE于点F.
的中点,CE⊥AB于E,BD交CE于点F. 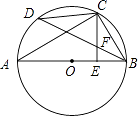
(1)求证:CF=BF;
(2)若CD=6,AC=8,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com