
| | 进价(元/台) | 售价(元/台) |
| 电视机 | 5000 | 5500 |
| 洗衣机 | 2000 | 2160 |
| 空 调 | 2400 | 2700 |
 台,根据商场计划的总费用11.8万元,空调的数量不超过电视机数量的三倍,即可列不等式组求解.
台,根据商场计划的总费用11.8万元,空调的数量不超过电视机数量的三倍,即可列不等式组求解. ,先表示出利润
,先表示出利润 关于x的函数关系式,再根据函数的性质即可判断.
关于x的函数关系式,再根据函数的性质即可判断. 台,由题意得
台,由题意得

 ,由题意得
,由题意得

 时,
时, 最大,为12600
最大,为12600

科目:初中数学 来源:不详 题型:解答题
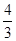 x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| P从点O出发 平移次数 | 可能到达的 点的坐标 |
| 1 次 | (0,2)(1,0) |
| 2 次 | |
| 3 次 | |

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 ),过x轴上的点1、3、5、7、9、11……分别作x轴的垂线,与直线OP相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn则Sn关于n的函数关系式是____.
),过x轴上的点1、3、5、7、9、11……分别作x轴的垂线,与直线OP相交得到一组梯形,其阴影部分梯形的面积从左至右依次记为S1、S2、S3……Sn则Sn关于n的函数关系式是____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com