
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФЖЅЕуOдкзјБъдЕуЃЌЖЅЕуAЕФзјБъЮЊ(4ЃЌ3)ЃЎ
(1)ЖЅЕу![]() ЕФзјБъЮЊ( ЃЌ )ЃЛ
ЕФзјБъЮЊ( ЃЌ )ЃЛ
(2)ЯжгаЖЏЕуPЁЂQЗжБ№ДгCЁЂAЭЌЪБГіЗЂЃЌЕуPбиЯпЖЮCBЯђжеЕуBдЫЖЏЃЌЫйЖШЮЊУПУы1ИіЕЅЮЛЃЌЕуQбиелЯпAЁњOЁњCЯђжеЕуCдЫЖЏЃЌЫйЖШЮЊУПУыkИіЕЅЮЛЃЌЕБдЫЖЏЪБМфЮЊ2УыЪБЃЌвдPЁЂQЁЂCЮЊЖЅЕуЕФШ§НЧаЮЪЧЕШбќШ§НЧаЮЃЌЧѓДЫЪБkЕФжЕЃЎ
(3)Шєе§ЗНаЮOABCвдУПУы![]() ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕН
ИіЕЅЮЛЕФЫйЖШбиЩфЯпAOЯТЛЌЃЌжБжСЖЅЕуCТфЕН![]() жсЩЯЪБЭЃжЙЯТ
жсЩЯЪБЭЃжЙЯТ
ЛЌЃЎЩше§ЗНаЮOABCдк![]() жсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМф
жсЯТЗНВПЗжЕФУцЛ§ЮЊSЃЌЧѓSЙигкЛЌааЪБМф![]() ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСП
ЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіЯргІздБфСП![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ


(БИгУЭМ)
ЁОД№АИЁП(1)C(Ѓ3ЃЌ4)(2) kЕФжЕЮЊ2Лђ4(3)Ђй![]() Ђк
Ђк![]() ЃЈ3ЃМtЁм4ЃЉ
ЃЈ3ЃМtЁм4ЃЉ
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉШчЭМ1жаЃЌзї![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() жсгкNЃЎвзжЄ
жсгкNЃЎвзжЄ![]() Ёе
Ёе![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЭЦГі
ЭЦГі![]()
ЃЈ2ЃЉЗжСНжжЧщаЮЂйЕБЕуQдкOAЩЯЪБЃЎЂкЕБЕуQдкOCЩЯЪБЃЎЗжБ№МЦЫуМДПЩЃЎ
ЃЈ3ЃЉЗжСНжжЧщаЮЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3ЃЌЕБ0<tЁм3ЪБЃЌЩш![]() НЛxжсгкЕуEЃЌзї
НЛxжсгкЕуEЃЌзї![]() жсгкЕуFЃЈШчЭМ3жаЃЉЃЎЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4ЕБ3<tЁм4ЪБЃЈШчЭМ4жаЃЉЃЌЩш
жсгкЕуFЃЈШчЭМ3жаЃЉЃЎЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4ЕБ3<tЁм4ЪБЃЈШчЭМ4жаЃЉЃЌЩш![]() НЛxжсгкЕуFЃЎЗжБ№ЧѓНтМДПЩЃЎ
НЛxжсгкЕуFЃЎЗжБ№ЧѓНтМДПЩЃЎ
ЯъНтЃК(1)ШчЭМ1жаЃЌзїCMЁЭxжсгкЃЌANЁЭxжсгкN.
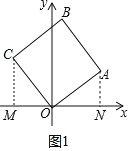
взжЄЁїAONЁеЁїCOMЃЌПЩЕУCM=ON=4ЃЌOM=AN=3ЃЌ
Ёр![]()
(2)гЩЬтвтЕУЃЌAO=CO=BC=AB=5ЃЌ
ЕБt=2ЪБЃЌCP=2.
ЂйЕБЕуQдкOAЩЯЪБЃЌ![]() ЃЌ
ЃЌ
ЁржЛДцдквЛЕуQЃЌЪЙQC=QP.
зїQDЁЭPCгкЕуD(ШчЭМ2жа)ЃЌдђCD=PD=1ЃЌ
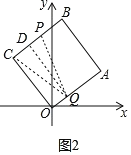
ЁрQA=2k=51=4ЃЌ
Ёрk=2.
ЂкЕБЕуQдкOCЩЯЪБ,гЩгкЁЯC=90ЫљвджЛДцдквЛЕуQЃЌЪЙCP=CQ=2ЃЌ
Ёр2k=102=8ЃЌЁрk=4.
злЩЯЫљЪіЃЌkЕФжЕЮЊ2Лђ4.
(3)ЂйЕБЕуAдЫЖЏЕНЕуOЪБЃЌt=3.
ЕБ![]() ЪБ,ЩшOЁЏCЁЏНЛxжсЕуE,зїAЁЏFЁЭxжсгкЕуF(ШчЭМ3жа).
ЪБ,ЩшOЁЏCЁЏНЛxжсЕуE,зїAЁЏFЁЭxжсгкЕуF(ШчЭМ3жа).
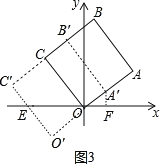
дђЁїAЁЏOFЁзЁїEOOЁЏЃЌ
ЁрЁр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() .
.
![]() .(
.(![]() ).
).
ЂкЕБЕуCдЫЖЏЕНxжсЩЯЪБЃЌt=4
ЕБ![]() ЪБ(ШчЭМ4жа)ЃЌЩшAЁЏBЁЏНЛxжсгкЕуFЃЌ
ЪБ(ШчЭМ4жа)ЃЌЩшAЁЏBЁЏНЛxжсгкЕуFЃЌ
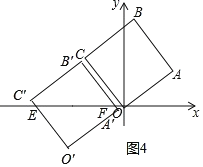
дђдђAЁЏO=![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёр![]() .(
.(![]() ).
).
злЩЯЫљЪі,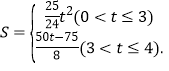


 аТЬтаЭШЋГЬМьВтЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аТЬтаЭШЋГЬМьВтЦкФЉГхДЬ100ЗжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИажЊгыЬюПе:ШчЭМЂйЃЌжБЯп![]() ЃЌЧѓжЄ:
ЃЌЧѓжЄ:![]() .
.
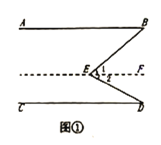
дФЖСЯТУцЕФНтД№Й§ГЬЃЌВЂЬюЩЯЪЪЕБЕФРэгЩЃЌ
Нт:Й§Еу![]() зїжБЯп
зїжБЯп![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() (вбжЊ)ЃЌ
(вбжЊ)ЃЌ![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
![]() ,
,
![]() ЃЈ ЃЉ
ЃЈ ЃЉ
гІгУгыЭиеЙ:ШчЭМЂкЃЌжБЯп![]() ЃЌШє
ЃЌШє![]() .
.
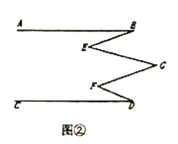
дђ![]() ЖШ
ЖШ
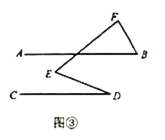
ЗНЗЈгыЪЕМљ:ШчЭМЂлЃЌжБЯп![]() ЃЌШє
ЃЌШє![]() ,дђ
,дђ![]() ЖШ.
ЖШ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈжаЃЌе§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
ЂйСНЕужЎМфЃЌжБЯпзюЖЬ.
ЂкШ§ЬѕжБЯпСНСНЯрНЛЃЌзюЩйгаШ§ИіНЛЕу.
ЂлЩфЯп![]() КЭЩфЯп
КЭЩфЯп![]() ЪЧЭЌвЛЬѕЩфЯп.
ЪЧЭЌвЛЬѕЩфЯп.
ЂмЭЌНЧЃЈЛђЕШНЧЃЉЕФВЙНЧЯрЕШ.
ЂндкЭЌвЛЦНУцФкЃЌДЙжБгкЭЌвЛЬѕжБЯпЕФСНЬѕжБЯпЛЅЯрЦНаа.
ЂоОјЖджЕЕШгкЫќБОЩэЕФЪ§ЪЧЗЧИКЪ§.
A.![]() ИіB.
ИіB.![]() ИіC.
ИіC.![]() ИіD.
ИіD.![]() Иі
Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпABЁЂCDЯрНЛгкЕуOЃЌвбжЊЁЯAOC=75ЁуЃЌЁЯBOE ЃКЁЯDOE=2:3ЃЎ

ЃЈ1ЃЉЧѓЁЯBOEЕФЖШЪ§ЃЛ
ЃЈ2ЃЉШєOFЦНЗжЁЯAOEЃЌЁЯAOCгыЁЯAOFЯрЕШТ№ЃПЮЊЪВУД?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌOЮЊвЛИіФЃФтжгУцдВаФЃЌMЁЂOЁЂN дквЛЬѕжБЯпЩЯЃЌжИеы OAЁЂOB ЗжБ№Дг OMЁЂON ГіЗЂШЦЕу O зЊЖЏЃЌOA дЫЖЏЫйЖШЮЊУПУы 30ЁуЃЌOB дЫЖЏЫйЖШЮЊУПУы10ЁуЃЌЕБвЛИљжИеыгыЦ№ЪМЮЛжУжиКЯЪБЃЌдЫЖЏЭЃжЙЃЌЩшзЊЖЏЕФЪБМфЮЊ t УыЃЌЪдНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉШчЭМЂйЃЌШєOAЫГЪБеызЊЖЏЃЌOBФцЪБеызЊЖЏЃЌ![]() = ЁЁЁЁ УыЪБЃЌOAгыOBЕквЛДЮжиКЯЃЛ
= ЁЁЁЁ УыЪБЃЌOAгыOBЕквЛДЮжиКЯЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌШєOAЁЂOBЭЌЪБЫГЪБеызЊЖЏЃЌ
ЂйЕБ![]() =3УыЪБЃЌЁЯAOB= ЁЁЁЁ ЁуЃЛ
=3УыЪБЃЌЁЯAOB= ЁЁЁЁ ЁуЃЛ
ЂкЕБ![]() ЮЊКЮжЕЪБЃЌШ§ЬѕЩфЯпOAЁЂOBЁЂONЦфжавЛЬѕЩфЯпЪЧСэСНЬѕЩфЯпМаНЧЕФНЧЦНЗжЯпЃП
ЮЊКЮжЕЪБЃЌШ§ЬѕЩфЯпOAЁЂOBЁЂONЦфжавЛЬѕЩфЯпЪЧСэСНЬѕЩфЯпМаНЧЕФНЧЦНЗжЯпЃП



ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдквЛеХГЄЗНаЮжНЬѕЩЯЛвЛЬѕЪ§жсЃЎ

ЃЈ1ЃЉШєелЕўжНЬѕЪЙЪ§жсЩЯБэЪОЉ1ЕФЕугыБэЪО5ЕФЕужиКЯЃЌдђелКлгыЪ§жсЕФНЛЕуБэЪОЕФЪ§ЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉШчЙћЪ§жсЩЯСНЕужЎМфЕФОрРыЮЊ6+m2ЃЈmЮЊГЃЪ§ЃЉЃЌетСНЕуОЙ§ЃЈ1ЃЉЕФелЕўЗНЪНКѓелКлгыЪ§жсЕФНЛЕугыЃЈ1ЃЉжаЕФНЛЕуЯрЭЌЃЌЧѓзѓБпетИіЕуБэЪОЕФЪ§ЃЛЃЈгУКЌmЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ3ЃЉШчЭМ2ЃЌШєНЋДЫжНЬѕбиAЃЌBДІМєПЊЃЌНЋжаМфЕФвЛЖЮжНЬѕЖделЃЌЪЙЦфзѓгвСНЖЫжиКЯЃЌетбљСЌајЖделnДЮКѓЃЌдйНЋЦфеЙПЊЃЌЧѓзюгвЖЫЕФелКлгыЪ§жсЕФНЛЕуБэЪОЕФЪ§ЃЎЃЈгУКЌnЕФДњЪ§ЪНБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаЕШЪНЃК
Ек1ИіЕШЪНЃКa1ЃН![]()
Ек2ИіЕШЪНЃКa2ЃН![]()
Ек3ИіЕШЪНЃКa3ЃН![]()
Ек4ИіЕШЪНЃКa4ЃН![]() Ё
Ё
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉАДвдЩЯЙцТЩСаГіЕк5ИіЕШЪНЃКa5ЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉгУКЌгаnЕФДњЪ§ЪНБэЪОЕкnИіЕШЪНЃКanЃНЁЁ ЁЁЃЈnЮЊе§ећЪ§ЃЉЃК
ЃЈ3ЃЉЧѓa1+a2+a3+a4+ЁЁ+a100ЕФжЕЃЛ
ЃЈ4ЃЉЬНОПМЦЫуЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛИіВЛЭИУїЯфзгжага2ИіКьЧђЃЌ1ИіКкЧђКЭ1ИіАзЧђЃЌЫФИіаЁЧђЕФаЮзДЁЂДѓаЁЭъШЋЯрЭЌЃЎ
ЃЈ1ЃЉДгжаЫцЛњУўШЁ1ИіЧђЃЌдђУўЕНКкЧђЕФИХТЪЮЊ ЃЛ
ЃЈ2ЃЉаЁУїКЭаЁБДзіУўЧђгЮЯЗЃЌгЮЯЗЙцдђШчЯТЃЎ

ФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОЛѕГЕДгАйЛѕДѓТЅГіЗЂИКд№ЫЭЛѕЃЌЯђЖЋзпСЫ4ЧЇУзЕНДяаЁУїМвЃЌМЬајЯђЖЋзпСЫ1.5ЧЇУзЕНДяаЁКьМвЃЌШЛКѓЯђЮїзпСЫ8.5ЧЇУзЕНДяаЁИеМвЃЌзюКѓЗЕЛиАйЛѕДѓТЅ.

ЃЈ1ЃЉвдАйЛѕДѓТЅЮЊдЕуЃЌЯђЖЋЮЊе§ЗНЯђЃЌ1ИіЕЅЮЛГЄЖШБэЪО1ЧЇУзЃЌЧыФудкЪ§жсЩЯБъГіаЁУїЁЂаЁКьЁЂаЁИеМвЕФЮЛжУ.ЃЈаЁУїМвгУЕу![]() БэЪОЃЌаЁКьМвгУЕу
БэЪОЃЌаЁКьМвгУЕу![]() БэЪОЃЌаЁИеМвгУЕу
БэЪОЃЌаЁИеМвгУЕу![]() БэЪОЃЉ
БэЪОЃЉ
ЃЈ2ЃЉаЁУїМвгыаЁИеМвЯрОрЖрдЖЃП
ЃЈ3ЃЉШєЛѕГЕУПЧЇУзКФгЭ1.5Щ§ЃЌФЧУДетСОЛѕГЕДЫДЮЫЭЛѕЙВКФгЭЖрЩйЩ§ЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com