
| 薄板的边长(cm) | 20 | 30 |
| 出厂价(元/张) | 50 | 70 |
分析 (1)利用待定系数法求一次函数解析式即可得出答案;
(2)①首先假设一张薄板的利润为W元,它的成本价为mx2元,由题意,得:W=y-mx2,进而得出m的值,求出函数解析式即可;
②利用二次函数的最值公式求出二次函数的最值即可.
解答 解:(1)设一张薄板的边长为xcm,它的出厂价为y元,基础价为n元,浮动价为kx元,则y=kx+n.
由表格中的数据,得$\left\{\begin{array}{l}{50=20k+n}\\{70=30k+n}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=2}\\{n=10}\end{array}\right.$,
所以y与边长x之间满足的函数关系式为:y=2x+10(5≤x≤50);
(2)①设一张薄板的利润为W元,它的成本价为mx2元,由题意,得:
W=y-mx2=2x+10-mx2,
将x=40,W=26代入W=2x+10-mx2中,
得26=2×40+10-m×402.
解得:m=$\frac{1}{25}$.
所以W=-$\frac{1}{25}$x2+2x+10.
②因为a=-$\frac{1}{25}$<0,所以,当x=-$\frac{b}{2a}$=-$\frac{2}{2×(-\frac{1}{25})}$═25(在5~50之间)时,
W最大值=$\frac{4ac-{b}^{2}}{4a}$=$\frac{4×(-\frac{1}{25})×10-{2}^{2}}{4×(-\frac{1}{25})}$=35.
即出厂一张边长为25cm的薄板,获得的利润最大,最大利润是35元.
点评 本题考查了二次函数的最值求法以及待定系数法求一次函数解析式,求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
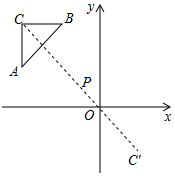 如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )
如图,△ABC的顶点坐标分别为A(-4,2),B(-2,4),C(-4,4),以点P(-1,1)为位似中心,将△ABC缩小后得到△A′B′C′.若点C的对应点C′的坐标为(2,-2),则点A的对应点A′的坐标为( )| A. | (2,0) | B. | (2,-1) | C. | (0,-2) | D. | (1,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:
小龙在学校组织的社会调查活动中负责了解他所居住的小区440户居民的家庭收入情况.他从中随机调查了40户居民家庭的人均月收入(收入取整数,单位:元),并绘制了频数分布表和频数分布直方图(如图).根据以上信息,解答下列问题:| 分组 | 频数 | 频率 |
| 600~799 | 2 | 0.050 |
| 800~999 | 6 | 0.150 |
| 1000~1199 | 18 | 0.450 |
| 1200~1399 | 9 | 0.225 |
| 1400~1599 | 3 | 0.075 |
| 1600~1800 | 2 | 0.050 |
| 合计 | 40 | 1.000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
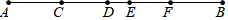 如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.
如图,C、D、E、F为线段AB上顺次排列的4个动点(不与A、B重合),图中共有15条线段.若AB=8.6cm,DE=1cm,图中所有线段长度之和为56cm,则线段CF长为4cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com