
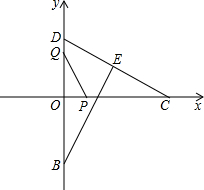
 (2013•瑞安市模拟)如图,在直角坐标系中,点C(
(2013•瑞安市模拟)如图,在直角坐标系中,点C(| 3 |
| 3 |
3
| ||
| 2 |
| 3 |
| 4 |
3
| ||
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| OP |
| OD |
| OQ |
| OC |
| OP |
| OC |
| OQ |
| OD |
| 3 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
3
| ||
| 2 |
| 3 |
| 4 |
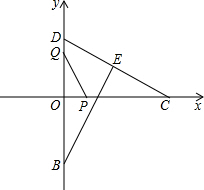 解:(1)由题意得:OD=1,OC=
解:(1)由题意得:OD=1,OC=| 3 |
|
| 3 |
| 3 |
| 3 |
| OP |
| OD |
| OQ |
| OC |
| OP |
| OC |
| OQ |
| OD |
| ||||
| 1 |
| t | ||
|
| ||||
|
| t |
| 1 |
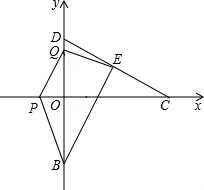 解得t=
解得t=| 3 |
| 7 |
| 1 |
| 3 |
| OP |
| OD |
| OQ |
| OC |
| OP |
| OC |
| OQ |
| OD |
2
| ||||
| 1 |
| t | ||
|
2
| ||||
|
| t |
| 1 |
| 3 |
| 5 |
| 3 |
| 7 |
| 1 |
| 3 |
| 3 |
| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
3
| ||
| 4 |
| ||
| 4 |
| 3 |
3
| ||
| 4 |
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
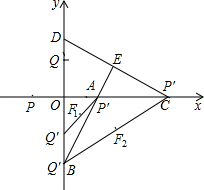 (4)①当P'Q'与BE有公共点时,初始位置点P′与点A重合,A为BE与x轴的交点.
(4)①当P'Q'与BE有公共点时,初始位置点P′与点A重合,A为BE与x轴的交点.
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
3
| ||
| 2 |
| 3 |
| 4 |
3
| ||
| 2 |
| 3 |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•瑞安市模拟)如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).
(2013•瑞安市模拟)如图,在边长为1的正方形组成的网格中建立直角坐标系,△AOB的顶点均在格点上,点O为原点,点A、B的坐标分别是A(3,2)、B(1,3).
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•瑞安市模拟)某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行.
(2013•瑞安市模拟)某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com