【题目】如图，已知正方形
的边长为4，边
在
轴上，边
在
轴上，点
是轴上一点，坐标为
，点
为的中点，连接
.
(1)点
的坐标为;
(2)判断
的形状，并证明你的结论.
【答案】(1)
； (2) 
为直角三角形.
【解析】
（1）利用正方形的性质得到BC=BA，然后利用第一象限点的坐标特征写出B点坐标；
（2）先利用勾股定理分别计算出DE、BE、BD，然后利用勾股定理的逆定理可证明△BDE为直角三角形.
（1）∵正方形ABCO的边长为4，
∴BC=BA=4，
∴B点坐标为（4，4）；
故答案为（4，4）；
（2）△BDE为直角三角形．理由如下：
∵D（1，0），点E为OC的中点，
∴OE=CE=2，OD=1，
∴AD=3，
∴DE2=OD2+OE2=1+4=5，BE2=CE2+BE2=4+16=20，DB2=AD2+AB2=9+16=25，
∵5+20=25，
∴DE2+BE2=DB2，
∴△BDE为直角三角形，∠BED=90°；
科目：初中数学 来源： 题型：
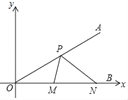
【题目】如图，∠AOB的边OB与x轴正半轴重合，点P是OA上的一动点，点N（6，0）是OB上的一定点，点M是ON的中点，∠AOB=30°，要使PM+PN最小，则点P的坐标为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
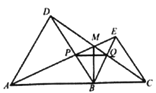
【题目】如图，点A，B，C在同一直线上，在这条直线同侧作等边△ABD和等边△BCE，连接AE和CD，交点为M，AE交BD于点P，CD交BE于点Q，连接PQ、BM， 有4个结论：①△ABE≌△DBC，②△DQB≌△ABP，③∠EAC=30°，④∠AMC=120°，请将所有正确结论的序号填在横线上______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知二次函数y=﹣x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（﹣1，0），与y轴的交点坐标为（0，3）．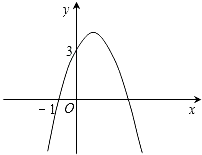 
（1）求出b，c的值，并写出此二次函数的解析式；
（2）根据图象，写出函数值y为正数时，自变量x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系
中，对于任意三点
的“矩面积”，给出如下定义:“水平底”
为任意两点横坐标差的最大值，“铅垂高”
为任意两点纵坐标差的最大值，则“矩面积”
.
例如:三点坐标分别为
，则“水平底”
，“铅垂高”
，“矩面积”
.
(1)已知点
.
①若
三点的“矩面积”为12，求点
的坐标;
②求三点的“矩面积”的最小值.
(2)已知点
，其中
.若
三点的“矩面积”为8，求
的取值范围.
查看答案和解析>>
科目：初中数学 来源： 题型：
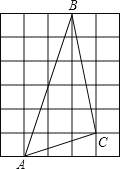
【题目】如图，图中的小方格都是边长为1的正方形，若点A(x，
)，点B(2x1，
)，点C(z+1，
)，已知点A，B关于原点对称，点C在二，四象限平分线上.
(1)求A、B、C点的坐标；
(2)结合A、B、C的坐标，在图中建立平面直角坐标系；
(3)在(2)的条件下，若P为y轴上的一个动点，请直接写出使△PBC周长最小的点P的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在一次中学生田径运动会上，根据参加男子跳高初赛的运动员的成绩（单位：m），绘制出如下的统计图①和图②，请根据相关信息，解答下列问题：
（Ⅰ）图1中a的值为 ；
（Ⅱ）求统计的这组初赛成绩数据的平均数、众数和中位数；
（Ⅲ）根据这组初赛成绩，由高到低确定9人进入复赛，请直接写出初赛成绩为1.65m的运动员能否进入复赛．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
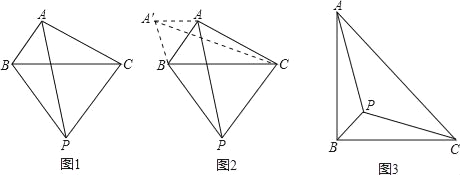
小伟遇到这样一个问题：如图1，在△ABC（其中∠BAC是一个可以变化的角）中，AB=2，AC=4，以BC为边在BC的下方作等边△PBC，求AP的最大值．
小伟是这样思考的：利用变换和等边三角形将边的位置重新组合．他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC，连接A′A，当点A落在A′C上时，此题可解（如图2）．
请你回答：AP的最大值是 ．
参考小伟同学思考问题的方法，解决下列问题：
如图3，等腰Rt△ABC．边AB=4，P为△ABC内部一点，则AP+BP+CP的最小值是 ．（结果可以不化简）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
