
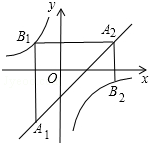
 如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1.
如图,已知点A1,A2,…,An均在直线y=x-1上,点B1,B2,…,Bn均在反比例函数y=-$\frac{1}{x}$的图象上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为an(n为正整数).若a1=-1,则a2017=-1. 分析 首先根据a1=-1,求出a2=2,a3=$\frac{1}{2}$,a4=-1,a5=2,…,所以a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$;然后用2017除以3,根据商和余数的情况,判断出a2016是第几个循环的第几个数,进而求出它的值是多少即可.
解答 解:∵a1=-1,
∴B1的坐标是(-1,1),
∴A2的坐标是(2,1),
即a2=2,
∵a2=2,
∴B2的坐标是(2,-$\frac{1}{2}$),
∴A3的坐标是($\frac{1}{2}$,-$\frac{1}{2}$),
即a3=$\frac{1}{2}$,
∵a3=$\frac{1}{2}$,
∴B3的坐标是($\frac{1}{2}$,-2),
∴A4的坐标是(-1,-2),
即a4=-1,
∵a4=-1,
∴B4的坐标是(-1,1),
∴A5的坐标是(2,1),
即a5=2,
…,
∴a1,a2,a3,a4,a5,…,每3个数一个循环,分别是-1、2、$\frac{1}{2}$,
∵2017÷3=672…1,
∴a2017是第673个循环的第1个数,
∴a2017=-1.
故答案为:-1.
点评 此题主要考查了反比例函数图象上点的坐标的特征,要熟练掌握,解答此题的关键是要明确:①图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;②双曲线是关于原点对称的,两个分支上的点也是关于原点对称;③在xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|;此题还考查了一次函数图象上的点的坐标特征,要熟练掌握,解答此题的关键是要明确:一次函数y=kx+b,(k≠0,且k,b为常数)的图象是一条直线.它与x轴的交点坐标是(-$\frac{b}{k}$,0);与y轴的交点坐标是(0,b).直线上任意一点的坐标都满足函数关系式y=kx+b.


科目:初中数学 来源: 题型:选择题
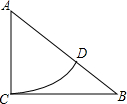 如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC长为半径作圆弧交边AB于点D.若 AC=3,BC=4.则BD的长是( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
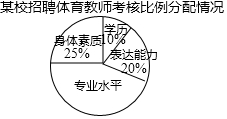 为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.
为贯彻国务院办公厅发布的《中国足球发展改革总体方案》精神,某校准备招聘一名足球专业的体育老师,该校对甲、乙、丙三名应聘者从学历、专业水平、身体素质、表达能力等四个方面考核打分,每一方面满分10分,得分情况如下表(单位:分),考核比例分配情况见扇形统计图.| 甲 | 乙 | 丙 | |
| 学历 | 8 | 9 | 8 |
| 专业水平 | 9 | 8 | 9 |
| 身体素质 | 8 | 7 | 6 |
| 表达能力 | 7 | 8 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
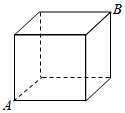 如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )
如图,一只昆虫在棱长为20cm的正方体的表面上爬行,则它从图中的顶点A爬到顶点B的最短距离为( )| A. | 40cm | B. | 60cm | C. | $20\sqrt{5}cm$ | D. | $40\sqrt{3}cm$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
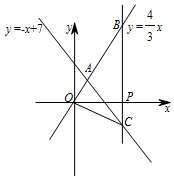 如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.
如图:在平面直角坐标系xOy中,已知正比例函数$y=\frac{4}{3}x$与一次函数y=-x+7的图象交于点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
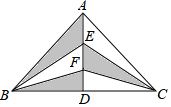 如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点E、F是高AD上的三等分点,则图中阴影部分的面积是( )
如图,在Rt△ABC中,∠BAC=90°,AB=AC=4,点E、F是高AD上的三等分点,则图中阴影部分的面积是( )| A. | 4 | B. | 8 | C. | 16 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com