
【题目】把一个足球垂直地面向上踢,![]() (秒)后该足球的高度
(秒)后该足球的高度![]() (米)适用公式
(米)适用公式![]() .
.
(1)经多少秒时足球的高度为20米?
(2)小明同学说:“足球高度不可能达到21米!”你认为他说得对吗?请说明理由.
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
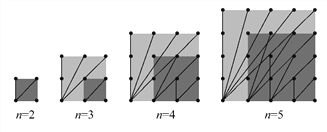
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师设计了一个数学实验,给甲、乙、丙三名同学各一张写有已化为最简(没有同类项)的代数式的卡片,规则是两位同学的代数式相减等于第三位同学的代数式,则实验成功,甲、乙、丙的卡片如下,丙的卡片有一部分看不清楚了.

(1)计算出甲减乙的结果,并判断甲减乙能否使实验成功;
(2)嘉琪发现丙减甲可以使实验成功,请求出丙的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列三行数:
0,3,8,15,24,…①
2,5,10,17,26,…②
0,6,16,30,48,…③
(1)第①行数按什么规律排的,请写出来?
(2)第②、③行数与第①行数分别对比有什么关系?
(3)取每行的第![]() 个数,求这三个数的和.
个数,求这三个数的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
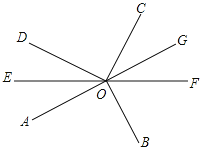
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
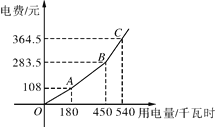
【题目】为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如图的折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是__________元;
(2)第二档的用电量范围是__________;
(3)“基本电价”是__________元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+3与两坐标轴交于A,B两点,抛物线y=﹣x2+bx+c过A、B两点,且交x轴的正半轴于点C.
(1)直接写出A、B两点的坐标;
(2)求抛物线的解析式和顶点D的坐标;
(3)在抛物线上是否存在点P,使得△PAB是以AB为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
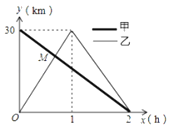
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
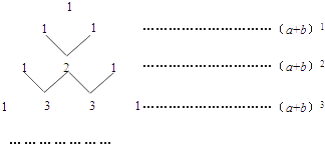
(1)根据上面的规律,则(a+b)5的展开式=________.
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1=________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com