
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

【答案】见解析
【解析】
(1)由A、B、C三点的坐标,利用待定系数法可求得抛物线解析式;
(2)当点D在x轴上方时,则可知当CD∥AB时,满足条件,由对称性可求得D点坐标;当点D在x轴下方时,可证得BD∥AC,利用AC的解析式可求得直线BD的解析式,再联立直线BD和抛物线的解析式可求得D点坐标;
(3)过点P作PH∥y轴交直线BC于点H,可设出P点坐标,从而可表示出PH的长,可表示出△PEB的面积,进一步可表示出直线AP的解析式,可求得F点的坐标,联立直线BC和PA的解析式,可表示出E点横坐标,从而可表示出△CEF的面积,再利用二次函数的性质可求得S1-S2的最大值.
(1)由题意可得 ,解得
,解得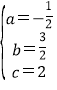 ,
,
∴抛物线解析式为y=-![]() ;
;
(2)当点D在x轴上方时,过C作CD∥AB交抛物线于点D,如图1,

∵A、B关于对称轴对称,C、D关于对称轴对称,
∴四边形ABDC为等腰梯形,
∴∠CAO=∠DBA,即点D满足条件,
∴D(3,2);
当点D在x轴下方时,
∵∠DBA=∠CAO,
∴BD∥AC,
∵C(0,2),
∴可设直线AC解析式为y=kx+2,把A(-1,0)代入可求得k=2,
∴直线AC解析式为y=2x+2,
∴可设直线BD解析式为y=2x+m,把B(4,0)代入可求得m=-8,
∴直线BD解析式为y=2x-8,
联立直线BD和抛物线解析式可得
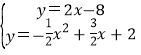 ,解得
,解得![]() 或
或![]() ,
,
∴D(-5,-18);
综上可知满足条件的点D的坐标为(3,2)或(-5,-18);
(3)过点P作PH∥y轴交直线BC于点H,如图2,
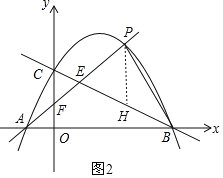
设P(t,-![]() t+2),
t+2),
由B、C两点的坐标可求得直线BC的解析式为y=- ![]() ,
,
∴H(t,-![]() ),
),
∴PH=yP-yH=-![]()
=-![]() ,
,
设直线AP的解析式为y=px+q,
∴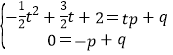 ,解得
,解得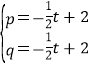 ,
,
∴直线AP的解析式为y=(-![]() t+2)(x+1),令x=0可得y=2-
t+2)(x+1),令x=0可得y=2-![]() t,
t,
∴F(0,2-![]() t),
t),
∴CF=2-(2-![]() t)=
t)=![]() t,
t,
联立直线AP和直线BC解析式可得
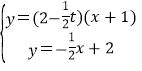 ,解得x=
,解得x=![]() ,即E点的横坐标为
,即E点的横坐标为![]() ,
,
∴S1=![]() PH(xB-xE)=
PH(xB-xE)=![]() (-
(-![]() t2+2t)(5-
t2+2t)(5-![]() ),S2=
),S2=![]()
![]()
![]() ,
,
∴S1-S2=![]() (-
(-![]() t2+2t)(5-
t2+2t)(5-![]() )-
)-![]()
![]()
![]() ,=-
,=-![]() t2+5t=-
t2+5t=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
∴当t=![]() 时,有S1-S2有最大值,最大值为
时,有S1-S2有最大值,最大值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,下面的结论: ①∠APO+∠DCO=30°;②△OPC是等边三角形;③AC=AO+AP;④S△ABC=S四边形AOCP,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的菱形
的菱形![]() 中,对角线
中,对角线![]() ,点
,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
如图,在边长为![]() 的菱形
的菱形![]() 中,对角线
中,对角线![]() ,点
,点![]() 是直线
是直线![]() 上的动点,
上的动点,![]() 于
于![]() ,
,![]() 于
于![]() .
.
![]() 对角线
对角线![]() 的长是________,菱形
的长是________,菱形![]() 的面积是________;
的面积是________;
![]() 如图
如图![]() ,当点
,当点![]() 在对角线
在对角线![]() 上运动时,
上运动时,![]() 的值是否发生变化?请说明理由;
的值是否发生变化?请说明理由;
![]() 如图
如图![]() ,当点
,当点![]() 在对角线
在对角线![]() 的延长线上时,
的延长线上时,![]() 的值是否发生变化?若不变请说明理由,若变化,请直接写出
的值是否发生变化?若不变请说明理由,若变化,请直接写出![]() 、
、![]() 之间的数量关系,不用明理由.
之间的数量关系,不用明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2,若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )
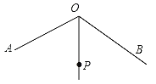
A.2个B.3个C.4个D.无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.
(1)甲、乙两种书柜每个的价格分别是多少元?
(2)若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量一河两岸相对电线杆![]() 、
、![]() 之间的距离,有四位同学分别测量出了一下四组数据:
之间的距离,有四位同学分别测量出了一下四组数据:
①![]() ,
,![]() ;②
;②![]() ,
,![]() ,
,![]() ;③
;③![]() ,
,![]() ,
,![]() ;④
;④![]() ,
,![]() ,
,![]() ;
;
能根据所测数据,求出![]() 、
、![]() 间距离的共有( )
间距离的共有( )

A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边的中点,DE⊥BC,∠ABC的角平分线BF交DE于点P,交AC于点M,连接PC.
(Ⅰ)若∠A=60°,∠ACP=24°,求∠ABP的度数;
(Ⅱ)若AB=BC,BM2+CM2=m2(m>0),△PCM的周长为m+2时,求△BCM的面积(用含m的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂里有许多剩余的三角形边角料,找出一块△ABC,测得∠C=90°(如图),现要从这块三角形上剪出一个半圆O,做成玩具,要求:使半圆O与三角形的两边AB、AC相切,切点分别为D、C,且与BC交于点E.
(1)在图中设计出符合要求的方案示意图.(要求:尺规作图,不写作法,保留作图痕迹).
(2)Rt△ABC中,AC=3,AB=5,连接AO,求出AO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,BE⊥AC于点E,AD与BE交于点F,BH⊥AB于点B,点M是BC的中点,连接FM并延长交BH于点H.

(1)如图①所示,若∠ABC=30°,求证:DF+BH=![]() BD;
BD;
(2)如图②所示,若∠ABC=45°,如图③所示,若∠ABC=60°(点M与点D重合),猜想线段DF、BH与BD之间又有怎样的数量关系?请直接写出你的猜想,不需证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com