
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】首先根据折叠可得CD=AC=3,BC=4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,然后求得△BCF是等腰直角三角形,进而求得∠B/GD=90°,CE-EF=![]() ,ED=AE=
,ED=AE=![]() ,
,
从而求得B/D=1,DF=![]() ,在Rt△B/DF中,由勾股定理即可求得B/F的长.
,在Rt△B/DF中,由勾股定理即可求得B/F的长.
解:根据首先根据折叠可得CD=AC=3,B/C=B4,∠ACE=∠DCE,∠BCF=∠B/CF,CE⊥AB,
∴BD=4-3=1,∠DCE+∠B/CF=∠ACE+∠BCF,
∴∠ACB=90°,∴∠ECF=45°,
∴△ECF是等腰直角三角形,
∴EF=CE,∠EFC=45°,
∴∠BFC=∠B/FC=135°,
∴∠B/FD=90°,
∵S△ABC=![]() AC×BC=
AC×BC=![]() AB×CE,
AB×CE,
∴AC×BC=AB×CE,
∵根据勾股定理求得AB=5,
∴CE=![]() ,∴EF=
,∴EF=![]() ,ED=AE=
,ED=AE=![]() =
=![]()
∴DE=EF-ED=![]() ,
,
∴B/F=![]() =
=![]() .
.
故答案为: ![]()
“点睛”此题主要考查了翻折变换,等腰三角形的判定和性质,勾股定理的应用等,根据折叠的性质求得相等的角是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我校学生会准备调查七年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数:
(1)确定调查方式时,甲同学说:“我到七年级(1)班去调查全体同学”;乙同学说:“放学时我到校门口随机调查部分同学”;丙同学说:“我到七年级每个班随机调查一定数量的同学”。请你指出哪位同学的调查方式最合理:
(2)他们采用了最为合理的调查方法收集数据,并绘制了如图所示的统计表和扇形统计图。

请你根据以上图表提供的信息解答下列问题:
① a= , b= ;
②在扇形统计图中器乐类所对应扇形的圆心角的度数是 ;
③若我校七年级有学生480人,请你估计大约有多少学生参加武术类校本课程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育用品店购进一批单件为40元的球服,如果按单价60元销售样,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套.设销售单价为x(x≥60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单件为多少元时,月销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在线段上依次添加1个点,2个点,3个点,……,原线段上所成线段的总条数如下表:
添加点数 | 1 | 2 | 3 | 4 |
线段总条数 | 3 | 6 | 10 | 15 |
若在原线段上添加n个点,则原线段上所有线段总条数为( )
A. n+2 B. 1+2+3+…+n+n+1 C. n+1 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AOB是一条直线,∠1=∠2,∠3=∠4,∠AOF=∠BOF=90°.则
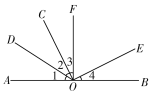
(1)∠AOC的补角是_____;
(2)____是∠AOC的余角;
(3)∠COF的补角是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c满足(a-![]() )2+
)2+![]() +
+![]() =0.
=0.
(1)求a,b,c的值.
(2)以a,b,c为边能否构成三角形?若能构成,求出该三角形的周长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知有理数a、b、c在数轴上对应的点如图所示,则下列结论正确的是( )
![]()
A. c+b>a+b B. cb<ab C. ﹣c+a>﹣b+a D. ac>ab
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师要为他家的长方形餐厅(如图1)选择一张餐桌,并且想按如下要求摆放:餐桌一侧靠墙,靠墙对面的桌边留出宽度不小于80 cm的通道,另两边各留出宽度不小于60 cm的通道.那么在图2的四张餐桌中,其规格符合要求的餐桌编号是________.

图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com