
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,连接
上,连接![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,使点
翻折,使点![]() 落在同一平面内的点
落在同一平面内的点![]() 处.当
处.当![]() 与
与![]() 的直角边垂直时,
的直角边垂直时,![]() 的长为__________.
的长为__________.

【答案】1或![]()
【解析】
分两种情况讨论,当A′D⊥AC时,易证A′D∥BC,A′C⊥AB,△BCH∽△BAC,求得CH和A′H的长,再证得△A′HD∽△CHB,,求得A′D=1,即AD=1;当A′D⊥BC时,则A′D∥AC,AD=A′D,AC=A′C,∠ACD=∠A′CD,推出∠A′DC=∠A′CD,则A′D=A′C,即可求得答案.
在Rt△ABC中,AB=4,BC=3,
∴![]() ,
,
如图,当A′D⊥AC,
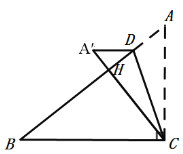
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴∠A′=∠A,A′D=AD,A′C=AC,
∵BC⊥AC,
∴A′D∥BC,
∠A′=∠A′CB =∠A,
∵∠B=∠B,
∴△BCH∽△BAC,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵A′D∥BC,
∴△A′HD∽△CHB,
∴![]() ,即
,即 ,
,
解得:A′D=1,
∴AD=1;
如图,当A′D⊥BC时,则A′D∥AC,
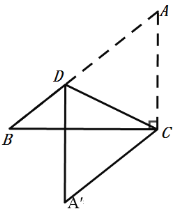
∵把△ACD沿直线CD折叠,点A落在同一平面内的A′处,
∴AD=A′D,AC=A′C,∠ACD=∠A′CD,
∵A′D∥AC,
∴∠A′DC=∠ACD,
∴∠A′DC=∠A′CD,
∴A′D=A′C,
∴AD=AC=![]() ,
,
综上所述:AD的长为:1或![]() ,
,
故答案为:1或![]() .
.


科目:初中数学 来源: 题型:
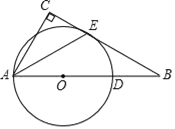
【题目】如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空并完成推理过程.
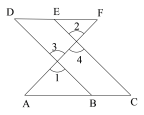
如图,E点为DF上的点,B点为AC上的点,∠1=∠2,∠C=∠D,试说明:AC∥DF.
证明:∵∠1=∠2(已知)
∠1=∠3(对顶角相等)
∴∠2=∠3( )
∴____∥______( )
∴∠C=∠ABD( )
又∵∠C=∠D(已知)
∴∠D=∠ABD(等量代换)
∴AC∥DF( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 由
由![]() 绕点
绕点![]() 顺时针旋转得到,其中点
顺时针旋转得到,其中点![]() 与点
与点![]() 、点
、点![]() 与点
与点![]() 是对应点,连接
是对应点,连接![]() ,且
,且![]() 、
、![]() 、
、![]() 在同一条直线上,则
在同一条直线上,则![]() 的长为( )
的长为( )

A. 3 B. ![]() C. 4 D.
C. 4 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:① abc>0;② 2a+b=0;③ 当m≠1时,a+b>am2+bm;④ a-b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,x1+x2=2,
其中正确的有( )

A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料并填空:
①(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() =(1﹣
=(1﹣![]() )(1+
)(1+![]() )=
)=![]() ×
×![]() ;
;
②(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() =(1﹣
=(1﹣![]() )(1+
)(1+![]() )= × ;
)= × ;
③(1﹣![]() )(1+
)(1+![]() )=1﹣
)=1﹣![]() ,反过来,得1﹣
,反过来,得1﹣![]() = =
= =![]() ;
;
利用上面的材料中的方法和结论计算下题:
(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )……(1﹣
)……(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EF的长为( )

A.6 B.12 C.2![]() D.4
D.4![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com