
已知,如图所示,P是⊙O直径AB延长线上一点,割线PCD交⊙O于C、D两点,弦DF⊥AB于H,CF交AB于点E,
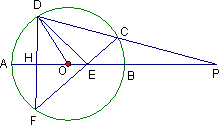
(1)求证:∠AOD=∠DCF;
(2)PA·PB=PO·PE;
若DE⊥CF,∠P=15°,⊙O的半径为2,求弦CF的长;
|
(1)∵AB是⊙O的直径,暇DF⊥AB于D点H, ∴弧AD=弧AF= ∴∠1=∠2 即:∠AOD=∠DCF (2)∵∠1=∠2, ∴∠POD=∠PCE ∵∠DPO=∠EPC ∴⊿DPO∽∠EPC ∴ ∵ ∴ (3)由(1)知: AB是弦DF的垂直平分线 ∴DE=EF, ∴∠3=∠4 ∵DE⊥CF ∴∠3=∠4= ∴∠4=∠5= ∵∠P= ∴∠1= 在Rt⊿DHO中, ∵∠1= ∴OH=1,DH= ∵DHE是等腰直角三角形 ∴DE= 又∵∠1=∠2,∠DHO=∠DEC= ∴∠DEO∽∠DEC ∴ ∴ ∴EC= ∴CF=CE+EF=CE+DE= |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com