练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

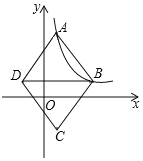
    【题目】如图，在平面直角坐标系中，菱形ABCD的顶点A、B在反比例函数y(k＞0，x＞0)的图象上，横坐标分别为1，4，对角线BD∥x轴，若菱形ABCD的面积为9．则k的值为____．

    【答案】2．

    【解析】

    根据题意，利用面积法求出AE，设出点B坐标，表示点A的坐标．应用反比例函数上点的横纵坐标乘积为k构造方程求k．

    连接AC分别交BD、x轴于点E、F．

    由已知，A、B横坐标分别为1，4，

    ∴BE=3．

    ∵四边形ABCD为菱形，AC、BD为对角线，

    ∴S菱形ABCD=4AEBE=9，

    ∴AE，设点B的坐标为(4，y)，则A点坐标为(1，y)

    ∵点A、B同在y图象上，

    ∴4y=1(y)，

    ∴y，

    ∴B点坐标为(4，)，

    ∴k=2

    故答案为：2．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各减去一个同样的小正方形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是32cm2，求剪去的小正方形的边长．设剪去的小正方形边长是xcm，根据题意可列方程为（　　）

    A. 10×6﹣4×6x=32 B. （10﹣2x）（6﹣2x）=32

    C. （10﹣x）（6﹣x）=32 D. 10×6﹣4x2=32

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，则点M的坐标为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

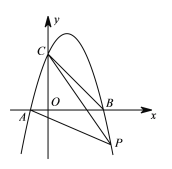
    【题目】如图抛物线经过点，tan∠CAB=3，且．

    （1）求抛物线的解析式及其对称轴；

    （2）点为抛物线上一点，连接，直线把四边形的面积分为两部分，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

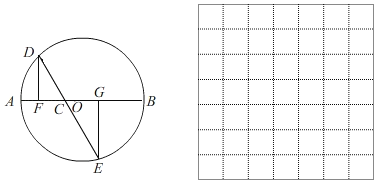
    【题目】如图，AB是⊙O的直径，AB=4cm，C为AB上一动点，过点C的直线交⊙O于D、E两点，且∠ACD=60°，DF⊥AB于点F，EG⊥AB于点G，当点C在AB上运动时，设AF=xcm，DE=ycm(当x的值为0或3时，y的值为2)，探究函数y随自变量x的变化而变化的规律．

    （1）通过取点、画图、测量，得到了x与y的几组对应值，如下表：

    x/cm

    0

    0.40

    0.55

    1.00

    1.80

    2.29

    2.61

    3

    y/cm

    2

    3.68

    3.84

    3.65

    3.13

    2.70

    2

    （2）建立平面直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

    （3）结合画出的函数图象，解决问题：点F与点O重合时，DE长度约为　　　　cm(结果保留一位小数)．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

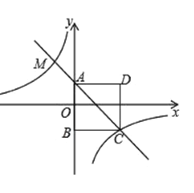
    【题目】如图，四边形为正方形.点的坐标为，点的坐标为，反比例函数的图象经过点，一次函数的图象经过点和点.

    （1）求反比例函数与一次函数的解析式；

    （2）写出的解集；

    （3）点是反比例函数图象上的一点，若的面积恰好等于正方形的面积，求点坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

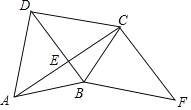
    【题目】如图，四边形ABCD的对角线AC⊥BD于点E，AB＝BC，F为四边形ABCD外一点，且∠FCA＝90°，∠CBF＝∠DCB．

    （1）求证：四边形DBFC是平行四边形；

    （2）如果BC平分∠DBF，∠F＝45°，BD＝2，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形是边长为1的正方形，与轴正半轴的夹角为15°，点在抛物线的图象上，则的值为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在同一直角坐标系中，二次函数的图象与两坐标轴分别交于点、点和点，一次函数的图象与抛物线交于，两点

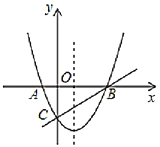
    （1）求二次函数的表达式；

    （2）当取什么值时，一次函数的函数值大于二次函数的函数值？

    查看答案和解析>>

    同步练习册答案