
)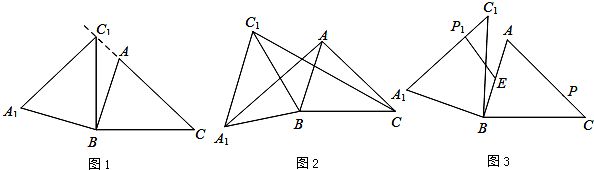 在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
在锐角△ABC中,AB=4,BC=5,∠ACB=45°,将△ABC绕点B按逆时针方向旋转,得到△A1BC1.
(1)如图1,当点C1在线段CA的延长线上时,求∠CC1A1的度数;
(2)如图2,连接AA1,CC1.若△ABA1的面积为4,求△CBC1的面积;
(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P 的对应点是点P1,求线段EP1长度的最大值与最小值.
的对应点是点P1,求线段EP1长度的最大值与最小值.
解:(1)由旋转的性质可得∠A1C1B =∠ACB =45°,BC=BC1
∴∠CC1B =∠C1CB =45°
∴∠CC1A1=∠CC1B+∠A1C1B=45°+45°=90°
(2)∵△ABC≌△A1BC1
∴BA=BA1,BC=BC1,∠ABC=∠A1BC1
∴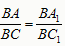 , ∠ABC+∠ABC1=∠A1BC1+∠ABC1
, ∠ABC+∠ABC1=∠A1BC1+∠ABC1
∴∠ABA1=∠CBC1
∴△ABA1∽△CBC1
∴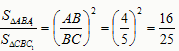
∵
∴
(3)过点B作BD⊥AC,D为垂足
∵△ABC为锐角三角形
∴点D在线段AC上Rt△BCD中,BD=BC×sin45°=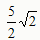
P在AC上运动至垂足点D,△ABC绕点B旋转,
使点P的对应点P1在线段AB上时,EP1最小,最小值为-2② 当P在AC上运动至点C,△ABC绕点B旋转,使点P的对应点P1在线段AB的延长线上时,EP1最大,最大值为2+5=7 。


科目:初中数学 来源: 题型:
在平面直角坐标系中,将抛物线y=3x2先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )
|
| A. | y=3(x+1)2+2 | B. | y=3(x+1)2﹣2 | C. | y=3(x﹣1)2+2 | D. | y=3(x﹣1)2﹣2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
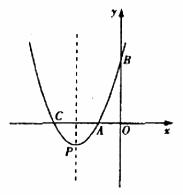
已知抛物线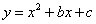 与x轴交于点
与x轴交于点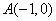 、C,与y轴交于点B(0,3),抛物线的顶点为p。
、C,与y轴交于点B(0,3),抛物线的顶点为p。
(1)求抛物线的解析式;
(2)若抛物线向下平移k个单位后经过点(-5,6)。
①求k的值及平移后抛物线所对应函数的最小值;
②设平移后抛物线与y轴交于点D,顶点为Q,点M是平移后的抛物线上的一个动点。请探究:当点M在何处时,△MBD的而积是△MPQ面积的2倍?求出此时点M的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是 ▲ ;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数 的概率.(请用“画树状图”或“列表”的方法写出过程)
的概率.(请用“画树状图”或“列表”的方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
宁波市轨道交通1号线一期工程批复总投资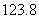 亿元,工程于2009年6月全面开工建设,工期为5年,到2014年通车试运营.
亿元,工程于2009年6月全面开工建设,工期为5年,到2014年通车试运营. 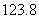 亿元用科学记数法表示为
亿元用科学记数法表示为
(A)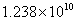 元 (B)
元 (B)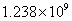 元 (C)
元 (C) 元 (D)
元 (D)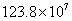 元
元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com