
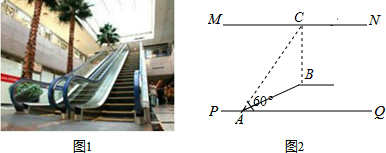
分析 延长CB交PQ于点D,根据自动扶梯AB的坡度为1:2可设BD=k,则AD=2k米,AB=$\sqrt{5}$k米.再由AB=5$\sqrt{5}$米求出k的值,故可得出BD及AD的长,在Rt△CDA中,根据锐角三角函数的定义求出CD的长,由BC=CD-BD即可得出结论.
解答 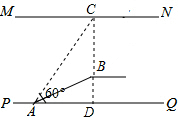 解:延长CB交PQ于点D,
解:延长CB交PQ于点D,
∵MN∥PQ,BC⊥MN,
∴BC⊥PQ.
∵自动扶梯AB的坡度为1:2,
∴$\frac{BD}{AD}$=$\frac{1}{2}$.
设BD=k,则AD=2k米,AB=$\sqrt{5}$k米.
∵AB=5$\sqrt{5}$米,
∴k=5,
∴BD=5米,AD=10米.
在Rt△CDA中,
∵∠CDA=90°,∠CAD=60°,
∴CD=AD•tan∠CAD=10×$\sqrt{3}$=10$\sqrt{3}$(米),
∴BC=CD-BD=(10$\sqrt{3}$-5)米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义是解答此题的关键.


科目:初中数学 来源: 题型:选择题
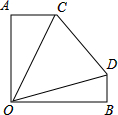 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )| A. | 90km | B. | 50$\sqrt{2}$km | C. | 20$\sqrt{13}$km | D. | 100km |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
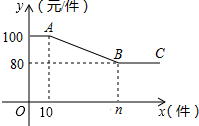 小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:
小颖妈妈的网店加盟了“小神龙”童装销售,有一款童装的进价为60元/件,售价为100元/件,因为刚加盟,为了增加销量,准备对大客户制定如下“促销优惠”方案:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
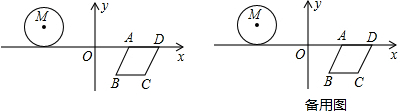
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,1) | B. | (8,4) | C. | (8,4)或(-8,-4) | D. | (2,1)或(-2,-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
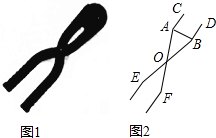 双十一期间,某店铺推出的如图1的雪球夹销售火爆,其形状可近似的看成图2的图形,当雪球夹闭合时,侧得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(结果精确到1厘米,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25.)
双十一期间,某店铺推出的如图1的雪球夹销售火爆,其形状可近似的看成图2的图形,当雪球夹闭合时,侧得∠AOB=28°,OA=OB=14厘米,求这个雪球夹制作的雪球的直径AB的长度.(结果精确到1厘米,参考数据:sin28°≈0.47,cos28°≈0.88,tan28°≈0.53,sin14°≈0.24,cos14°≈0.97,tan14°≈0.25.)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,BD为⊙O的直径,AB与⊙O相切于点B,连接AO,AO与⊙O交于点C,若∠A=30°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{4}{3}$π(结果保留π).
如图,BD为⊙O的直径,AB与⊙O相切于点B,连接AO,AO与⊙O交于点C,若∠A=30°,⊙O的半径为2,则$\widehat{CD}$的长为$\frac{4}{3}$π(结果保留π).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com