
| A�� | �٢� | B�� | �ڢ� | C�� | �ڢ� | D�� | �ۢ� |
���� ��������¼�����������塢���鷽ʽ���ʽ�ɣ���
��� �⣺���˽�ij��ѧ�������������Ҫ���ó��ķ�ʽ������
�ڼס������������У�S��2=0.5��S��2=0.3����IJ������Ҵ���ȷ��
��50�����п�����������������ͬ�������Խϴ���
������������ö�ʵؾ��ȵ�Ӳ�ң�����֡���ö���泯�ϡ�������ö���泯�ϡ�����һö���泯�ϣ�һö���泯�ϡ������¼�����ȷ��
��ѡC��
���� ���⿼����ȫ�������������飬��ȷ����ȫ���������������ǽ���ؼ���ע�����ʱ�¼����������ԵĴ�С������һ��������


 һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����A��2��n���ڷ���������y=$\frac{3}{x}$��ͼ���ϣ���B�ڵڶ����ޣ���AOB=90�㣬��OBA=30�㣬��С�����ѧϰ�У���λͬѧ���ֲ�����������ĸ����ۣ�������ȷ���У�����������
��ͼ����A��2��n���ڷ���������y=$\frac{3}{x}$��ͼ���ϣ���B�ڵڶ����ޣ���AOB=90�㣬��OBA=30�㣬��С�����ѧϰ�У���λͬѧ���ֲ�����������ĸ����ۣ�������ȷ���У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1.33��108 | B�� | 1.33��107 | C�� | 1.33��106 | D�� | 0.133��108 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��A��һ�κ���y=x��ͼ���뷴��������y=$\frac{2}{x}$��ͼ���ڵ�һ�����ڵĽ��㣬��B��x��ĸ���������OA=OB��
��ͼ����֪��A��һ�κ���y=x��ͼ���뷴��������y=$\frac{2}{x}$��ͼ���ڵ�һ�����ڵĽ��㣬��B��x��ĸ���������OA=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 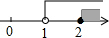 | B�� | 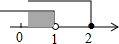 | C�� | 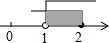 | D�� | 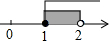 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
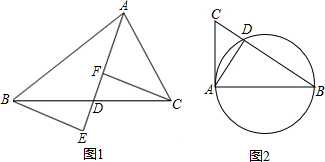
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | -3 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com