
分析 首先过点O作OD⊥AB于点C,交⊙O于点D,连接OA,由垂径定理即可求得AC的长,然后由勾股定理,求得OC的长,继而求得油面距底部的高度.
解答 解:过点O作OD⊥AB于点C,交⊙O于点D,连接OA, 由垂径定理得:AC=$\frac{1}{2}$AB=$\frac{1}{2}$×320=160(mm),
由垂径定理得:AC=$\frac{1}{2}$AB=$\frac{1}{2}$×320=160(mm),
在Rt△ACO中,AC2+OC2=AO2,
∴1602+OC2=2002,
解得:OC=120mm,
∴CD=OD-OC=200-120=80(mm).
答:油面距底部的高度是80mm.
点评 此题考查了垂径定理与勾股定理的应用.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{7}{20}$ | B. | ${-}\frac{7}{20}$ | C. | $\frac{7}{18}$ | D. | $-\frac{7}{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.
如图,六边形ABCDEF是正六边形,曲线FK1K2K3K4K5K6K7…叫做“正六边形的渐开线”,其中$\widehat{F{K}_{1}}$,$\widehat{{K}_{1}{K}_{2}}$,$\widehat{{K}_{2}{K}_{3}}$,$\widehat{{K}_{3}{K}_{4}}$,$\widehat{{K}_{4}{K}_{5}}$…的圆心依次按点A,B,C,D,E,F循环,分别记为l1,l2,l3,l4,l5,l6…当AB=1时,l2012等于$\frac{2012π}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F.
如图,在Rt△ACB中,∠C=90°,D是AB上一点,以BD为直径的⊙O切AC于点E,交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
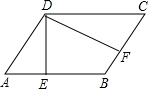 如图,李军家承包了一块菜地,用来种菜,菜地的形状为平行四边形.经测量其周长为36m,从钝角顶点处向AB、BC引的两条高DE、DF分别为5m、7m,求这块平行四边形菜地的面积.
如图,李军家承包了一块菜地,用来种菜,菜地的形状为平行四边形.经测量其周长为36m,从钝角顶点处向AB、BC引的两条高DE、DF分别为5m、7m,求这块平行四边形菜地的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com