
【题目】为了绿化环境,某中学八年级(3班)同学都积极参加了植树活动,下面是今年3月份该班同学植树情况的扇形统计图和不完整的条形统计图:
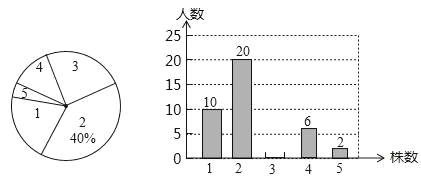
请根据以上统计图中的信息解答下列问题.
(1)植树3株的人数为 ;
(2)扇形统计图中植树为1株的扇形圆心角的度数为 ;
(3)该班同学植树株数的中位数是
(4)小明以下方法计算出该班同学平均植树的株数是:(1+2+3+4+5)÷5=3(株),根据你所学的统计知识
判断小明的计算是否正确,若不正确,请写出正确的算式,并计算出结果
【答案】(1)12;(2)72°;(3)2;(4)小明的计算不正确,2.4.
【解析】
(1)根据植树2株的人数及其所占的百分比计算出总人数,然后分别减去植树1株,2株,4株,5株的人数即可得到植树3株的人数;
(2)用360°乘以植树1株的人数所占的百分比即可得;
(3)根据中位数的定义可先计算植树的总人数,然后写出即可;
(4)根据平均数的定义判断计算即可.
解:(1)植树3株的人数为:20÷40%﹣10﹣20﹣6﹣2=12;
(2)扇形统计图中植树为1株的扇形圆心角的度数为:360°×![]() =72°;
=72°;
(3)植树的总人数为:20÷40%=50,
∴该班同学植树株数的中位数是2;
(4)小明的计算不正确,
正确的计算为:![]() =2.4.
=2.4.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
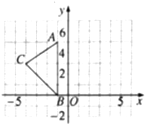
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,如图1,再在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒,底面为矩形EFGH,如图2.设小正方形的边长为x厘米.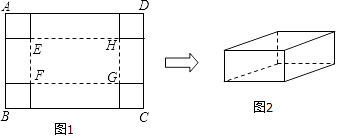
(1)当矩形纸板ABCD的一边长为90厘米时,求纸盒的侧面积的最大值;
(2)当EH:EF=7:2,且侧面积与底面积之比为9:7时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:小明热爱数学,在课外书上看到了一个有趣的定理﹣﹣“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2 . 小明尝试对它进行证明,部分过程如下:
解:过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2 ,
同理可得:AC2=AE2+CE2 , AD2=AE2+DE2 ,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=…
(1)请你完成小明剩余的证明过程;
理解运用: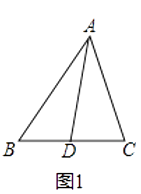
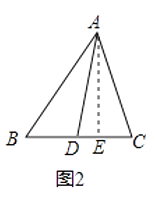
(2)①在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=;
②如图3,⊙O的半径为6,点A在圆内,且OA=2 ![]() ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为
拓展延伸: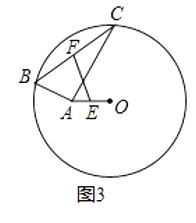
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5 ![]() ,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
,以A(﹣3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.
请你利用上面的方法和结论,求出AD长的最大值.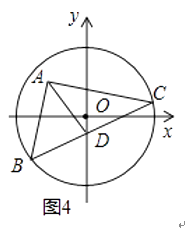
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线y=﹣![]() x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
x+6与y轴于点A,与x轴交于点D,直线AB交x轴于点B,△AOB沿直线AB折叠,点O恰好落在直线AD上的点C处.
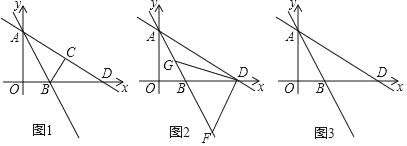
(1)求点B的坐标;
(2)如图2,直线AB上的两点F、G,△DFG是以FG为斜边的等腰直角三角形,求点G的坐标;
(3)如图3,点P是直线AB上一点,点Q是直线AD上一点,且P、Q均在第四象限,点E是x轴上一点,若四边形PQDE为菱形,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解“课程选修”的情况,对报名参加“艺术鉴赏”、“科技制作”、“数学思维”、“阅读写作”这四个选修项目的学生(每人限报一项)进行抽样调查.下面是根据收集的数据绘制的两幅不完整的统计图.
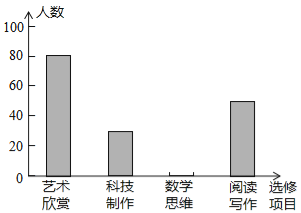
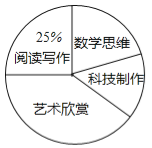
请根据图中提供的信息,解答下面的问题:
(1)此次共调查了 名学生,扇型统计图中“艺术鉴赏”部分的圆心角是 度.
(2)请把这个条形统计图补充完整.
(3)现该校共有800名学生报名参加这四个选修项目,请你估计其中有多少名学生选修“科技制作”项目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的身体素质,西南大学附中七年级学生在每天晚自习之后进行夜跑.在学期末的体育考试中,七年级的同学们表现出很好的体育素养,并取得了良好的体育成绩.为了了解七年级学生的体育考试情况,小明抽取了部分同学的体育考试成绩进行分析,体育成绩优、良、中、差分别记为![]() 并绘制了如下两幅不完整的统计表:
并绘制了如下两幅不完整的统计表:

(1)本次调查共调查了 名学生,并补全条形统计图;
(2)扇形统计图中![]() 类所对应的扇形圆心角的度数是 度;
类所对应的扇形圆心角的度数是 度;
(3)若七年级人数为![]() 人,请你估计体育成绩优、良的总人数.
人,请你估计体育成绩优、良的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两间工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com