
【题目】已知反比例函数 ![]() 的图象经过点
的图象经过点 ![]() ,若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
,若一次函数y=x+1的图象平移后经过该反比例函数图象上的点B(2,m),求平移后的一次函数图象与x轴的交点坐标.
科目:初中数学 来源: 题型:
【题目】如图,物理教师为同学们演示单摆运动,单摆左右摆动中,在OA的位置时俯角∠EOA=30°,在OB的位置时俯角∠FOB=60°,若OC⊥EF,点A比点B高7cm.求:
(1)单摆的长度( ![]() ≈1.7);
≈1.7);
(2)从点A摆动到点B经过的路径长(π≈3.1).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,椭圆 ![]() 的右顶点和上顶点分别为点A,B,M是线段AB的中点,且
的右顶点和上顶点分别为点A,B,M是线段AB的中点,且 ![]() ..
.. 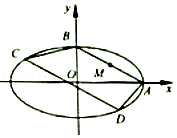
(1)求椭圆的离心率;
(2)若a=2,四边形ABCD内接于椭圆,AB∥CD,记直线AD,BC的斜率分别为k1 , k2 , 求证:k1k2为定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为( )
A.2cm
B.14cm
C.2cm或14cm
D.10cm或20cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q是反比例函数y= ![]() 图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”)
图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,△ABP的面积记为S1 , △QMN的面积记为S2 , 则S1S2 . (填“>”或“<”或“=”) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“任意画一个三角形,其内角和是360°”是随机事件
B.“明天的降水概率为80%”,意味着明天降雨的可能性较大
C.“某彩票中奖概率是1%”,表示买100张这种彩票一定会中奖
D.晓芳抛一枚硬币10次,有7次正面朝上,当她抛第11次时,正面向上的概率为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的3只球,球上分别标有2,3,5三个数字.
(1)从这个袋子中任意摸一只球,所标数字是奇数的概率是;
(2)从这个袋子中任意摸一只球,记下所标数字,不放回,再从从这个袋子中任意摸一只球,记下所标数字.将第一次记下的数字作为十位数字,第二次记下的数字作为个位数字,组成一个两位数.求所组成的两位数是5的倍数的概率.(请用“画树状图”或“列表”的方法写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a>0)的顶点为M,直线y=m与x轴平行,且与抛物线交于点A,B,若△AMB为等腰直角三角形,我们把抛物线上A,B两点之间的部分与线段AB围成的图形称为该抛物线对应的准碟形,线段AB称为碟宽,顶点M称为碟顶,点M到线段AB的剧烈为碟高.
(1)抛物线y=x2对应的碟宽为;抛物线y= ![]() x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
x2对应的碟宽为;抛物线y=ax2(a>0)对应的碟宽为;抛物线y=a(x﹣3)2+2(a>0)对应的碟宽为;
(2)利用图(1)中的结论:抛物线y=ax2﹣4ax﹣ ![]() (a>0)对应的碟宽为6,求抛物线的解析式.
(a>0)对应的碟宽为6,求抛物线的解析式.
(3)将抛物线yn=anx2+bnx+cn(an>0)的对应准蝶形记为Fn(n=1,2,3,…),定义F1 , F2 , …..Fn为相似准蝶形,相应的碟宽之比即为相似比.若Fn与Fn﹣1的相似比为 ![]() ,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
,且Fn的碟顶是Fn﹣1的碟宽的中点,现在将(2)中求得的抛物线记为y1 , 其对应的准蝶形记为F1 .
①求抛物线y2的表达式;
②若F1的碟高为h1 , F2的碟高为h2 , …Fn的碟高为hn . 则hn= , Fn的碟宽右端点横坐标为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com