
【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.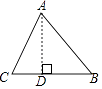
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
科目:初中数学 来源: 题型:
【题目】按图填空,并注明理由.
⑴完成正确的证明:如图,已知AB∥CD,求证:∠BED=∠B+∠D
证明:过E点作EF∥AB(经过直线外一点有且只有一条直线与这条直线平行)
∴∠1= ( )
∵AB∥CD(已知)
∴EF∥CD(如果两条直线与同一直线平行,那么它们也平行)
∴∠2= ( )
又∠BED=∠1+∠2
∴∠BED=∠B+∠D (等量代换).
⑵如图,在△ABC中,EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解:因为EF∥AD(已知)
所以∠2=∠3.( )
又因为∠1=∠2,所以∠1=∠3.(等量代换)
所以AB∥ ( )
所以∠BAC+ =180°( ).
又因为∠BAC=70°,所以∠AGD=110°.

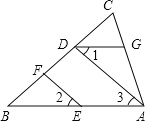
图⑴ 图⑵
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边△ABC内一点,连接PA,PB,PC,PA:PB:PC=3:4:5,以AC为边作△AP′C≌△APB,连接PP′,则有以下结论:①△APP′是等边三角形;②△PCP′是直角三角形;③∠APB=150°;④∠APC=105°.其中一定正确的是 . (把所有正确答案的序号都填在横线上) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com