
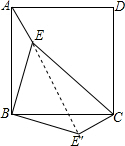
 如图,点E是正方形ABCD内的一点,点E′在BC边的下方,连接AE,BE,CE,BE′,CE′.若AE=1,BE=2,CE=3,且△ABE≌△CBE′,则∠BE′C=135°.
如图,点E是正方形ABCD内的一点,点E′在BC边的下方,连接AE,BE,CE,BE′,CE′.若AE=1,BE=2,CE=3,且△ABE≌△CBE′,则∠BE′C=135°. 分析 先由勾股定理的逆定理证得△EBE′是直角三角形,进而得出∠BEE′=∠BE′E=45°,即可得出答案.
解答 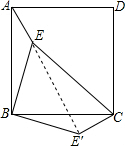 解:连接EE′
解:连接EE′
∵△ABE≌△CBE′,
∴∠ABE=∠CBE′,
∵四边形ABCD是正方形,
∴∠ABC=90°,
∴∠EBE′=90°,
∴△EBE′是直角三角形,
又∵△ABE≌△CBE′,
∴BE=BE′=2,∠AEB=∠BE′C
∴∠BEE′=∠BE′E=45°,
∵EE′2=22+22=8,AE=CE′=1,EC=3,
∴EC2=E′C2+EE′2,
∴△EE′C是直角三角形,
∴∠EE′C=90°,
∴∠AEB=135°,
故答案为:135.
点评 本题考查了正方形的性质、全等三角形的性质、勾股定理的逆定理;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com