
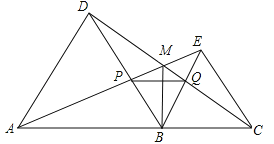
【题目】如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD,BD于点M,P,CD交BE于点Q,连接PQ,BM,下面结论:①△ABE≌△DBC;②∠DMA=60°;③△BPQ为等边三角形;④MB平分∠AMC,
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【答案】D.
【解析】
试题分析:∵△ABD、△BCE为等边三角形,∴AB=DB,∠ABD=∠CBE=60°,BE=BC,∴∠ABE=∠DBC,∠PBQ=60°,在△ABE和△DBC中,∵AB=DB,∠ABE=∠DBC,BE=BC,∴△ABE≌△DBC(SAS),∴①正确;
∵△ABE≌△DBC,∴∠BAE=∠BDC,∵∠BDC+∠BCD=180°﹣60°﹣60°=60°,∴∠DMA=∠BAE+∠BCD=∠BDC+∠BCD=60°,∴②正确;
在△ABP和△DBQ中,∵∠BAP=∠BDQ,AB=DB,∠ABP=∠ADBQ=60°,∴△ABP≌△DBQ(ASA),∴BP=BQ,∴△BPQ为等边三角形,∴③正确;
∵∠DMA=60°,∴∠AMC=120°,∴∠AMC+∠PBQ=180°,∴P、B、Q、M四点共圆,∵BP=BQ,∴![]() ,∴∠BMP=∠BMQ,即MB平分∠AMC,∴④正确;
,∴∠BMP=∠BMQ,即MB平分∠AMC,∴④正确;
综上所述:正确的结论有4个,故选D.


科目:初中数学 来源: 题型:
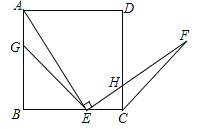
【题目】如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=![]() GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把方程x2+8x+7=0变形为(x+h)2=k的形式应为
A.(x+4)2=-7B.(x-4)2=-7C.(x+4)2=9D.(x-4)2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com