练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图所示，是一个几何体的三视图，已知正视图和左视图都是边长为2的等边三角形，则这个几何体的全面积为（ ）

    A．2л
    B．3л
    C．л
    D．（1+）л
    【答案】分析：易得此几何体为圆锥，那么全面积为：底面积+侧面积=π×底面半径2+π×底面半径×母线长．
    解答：解：此几何体为圆锥，底面直径为2，母线长为2，那么底面半径为1，
    ∴圆锥的全面积=π×12+π×1×2=3π，故选B．
    点评：主要考查了圆锥的全面积的公式；解决本题的关键是得到圆锥的底面直径与母线长．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

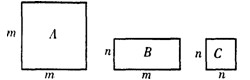    28、三种不同类型的矩形地砖长宽如图所示，若现有A类4块，B类4块，C类2块，要拼成一个正方形，则应多余出1块
    C
    型地砖；这样的地砖拼法表示了一个两数和的平方的几何意义，这个两数和的平方是
    （2m+n）2=4m2+4mn+n2
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

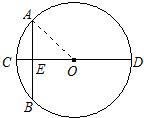    17、“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题，“今有圆材，埋壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何？”用现在的数学语言表述是：“如图所示，CD为⊙O的直径，CD⊥AB，垂足为E，CE=1寸，AB=1尺，求直径CD长是多少寸？”（注：1尺=10寸）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某公园中央地上有一个大理石球，小明想测量球的半径，于是找了两块厚10cm的砖塞在球的两侧（如图所示），他量了下两砖之间的距离刚好是60cm，聪明的你也能算出这个大石球的半径了吗？请你建立一个用于求大理石球的几何模型，并写出你的计算过程．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•西城区模拟）我们在几何的学习中能发现，很多图形的性质定理与判定定理之间有着一定的联系．例如：菱形的性质定理“菱形的对角线互相垂直”和菱形的判定定理“对角线互相垂直的平行四边形是菱形”就是这样．但是课本中对菱形的另外一个性质“菱形的对角线平分一组对角”却没有给出类似的判定定理，请你利用如图所示图形研究一下这个问题．
    要求：如果有类似的判定定理，请写出已知、求证并证明．如果没有，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

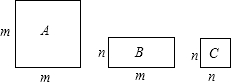    三种不同类型的长方形地砖长度如图所示，若有A型4块，B型4块，C型2块，要拼成一个正方形，则应多余出1块
    C
    C
    型地砖，这样的地砖拼法表示了一个两数和的平方的几何意义，这两个数的平方是
    （2m+n）2
    （2m+n）2
    （写成两数和的平方的形式）

    查看答案和解析>>

    同步练习册答案