
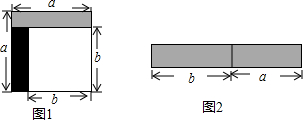
 从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).分析 (1)观察图1与图2,根据两图形阴影部分面积相等验证平方差公式即可;
(2)①已知第一个等式左边利用平方差公式化简,将第二个等式代入求出所求式子的值即可;②原式利用平方差公式变形,约分即可得到结果.
解答 解:(1)根据图形得:a2-b2=(a+b)(a-b),
上述操作能验证的等式是B,
故答案为:B;
(2)①∵x2-4y2=(x+2y)(x-2y)=12,x+2y=4,
∴x-2y=3;
②原式=(1-$\frac{1}{2}$)(1+$\frac{1}{2}$)(1-$\frac{1}{3}$)(1+$\frac{1}{3}$)…(1-$\frac{1}{49}$)(1+$\frac{1}{49}$)(1-$\frac{1}{50}$)(1+$\frac{1}{50}$)=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{48}{49}$×$\frac{50}{49}$×$\frac{49}{50}$×$\frac{51}{50}$=$\frac{1}{2}$×$\frac{51}{50}$=$\frac{51}{100}$.
点评 此题考查了平方差公式的几何背景,熟练掌握平方差公式是解本题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 用电量(度) | 120 | 140 | 160 | 180 | 200 |
| 户数 | 2 | 3 | 6 | 7 | 2 |
| A. | 180,180 | B. | 160,180 | C. | 160,160 | D. | 180,160 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com