(本题满分9分)将三角形纸片ABC(AB＞AC)沿过点A的直线折叠，使得AC落在AB边上，折痕为AD，展平纸片，如图(1)；再次折叠该三角形纸片，使得点A与点D重合，折痕为EF，再次展平后连接DE、DF，如图2，证明：四边形AEDF是菱形．
科目：初中数学 来源： 题型：
（本题满分7分）如图，在平面直角坐标系中，△ ABC的三个顶点的坐标分别为A（0,1），B（-1,1），C（-1,3）。
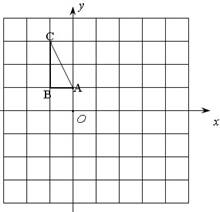
1.（1）画出△ABC关于x轴对称的△A1B1C1，并写出点C1的坐标；
2.（2）画出△ABC绕原点O顺时针方向旋转90°后得到的△A2B2C2，并写出点C2的坐标；，
3.（3）将△A2B2C2平移得到△ A3B3C3，使点A2的对应点是A3，点B2的对应点是B3 ，点C2的对应点是C3（4，-1），在坐标系中画出△ A3B3C3，并写出点A3，B3的坐标。
查看答案和解析>>
科目：初中数学 来源： 题型：
（本题满分8分）某市对九年级学生进行了一次学业水平测试，成绩评定分A、B、C、D四个等第．为了解这次数学测试成绩情况，相关部门从该市的农村、县镇、城市三类群体的学生中共抽取2 000名学生的数学成绩进行统计分析，相应数据的统计图表如下：
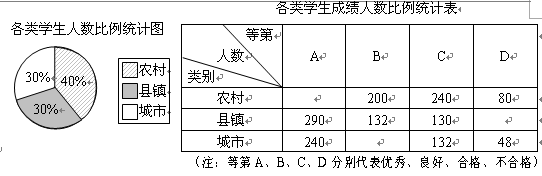
（1）请将上面表格中缺少的三个数据补充完整
（2）若该市九年级共有60 000名学生参加测试，试估计该市学生成绩合格以上（含合格）的人数．
查看答案和解析>>
科目：初中数学 来源：2010-2011学年广东省深圳市宝安区九年级第三次调研测试数学 题型：解答题
(本题满分10分)
如图所示，在直角坐标系中，平行四边形OABC的顶点坐标B（6，3），C（2，3）．
（1）求出过O、A、B三点的抛物线解析式；
（2）若直线
恰好将平行四边形OABC的面积分成相等的两部分，试求b的值
（3）若与
轴、y轴的交点分别记为M、N，（1）中抛物线的对称轴与此抛物
线及轴的交点分别记作点D、点E，试判断△OMN与△OED是否相似?
查看答案和解析>>
科目：初中数学 来源：2010年高级中等学校招生考试数学卷（江苏南通） 题型：解答题
(本题满分9分)
刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，
，
，
；图②中，
，
，
．图③是刘卫同学所做的一个实验：他将
的直角边
与
的斜边
重合在一起，并将沿方向移动．在移动过程中，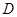
、
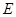两点始终在边上(移动开始时点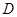与点
重合)．
(1)在沿方向移动的过程中，刘卫同学发现：
、
两点间的距离逐渐 ▲ ．
(填“不变”、“变大”或“变小”)
(2)刘卫同学经过进一步地研究，编制了如下问题：
问题①：当移动至什么位置，即
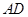的长为多少时，、的连线与
平行?
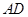问题②：当移动至什么位置，即的长为多少时，以线段、
、
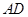的长度为三边长的三角形是直角三角形?
问题③：在的移动过程中，是否存在某个位置，使得
?如果存在，
求出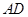的长度；如果不存在，请说明理由．
请你分别完成上述三个问题的解答过程．
查看答案和解析>>
科目：初中数学 来源：2011届江苏省江阴市九年级第二学期期中考试数学卷 题型：解答题
（本题满分10分）
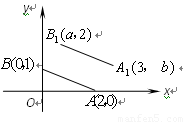
（一）探究：如图，A，B的坐标为（2，0），（0，1）若将线段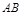
平移至
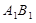，则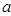
=
，
=
。
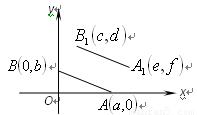
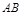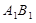（二）归纳：A，B的坐标为（a，0），（0，b）若将线段平移至，则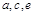
三者关系为
，
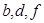三者间关系为 。
（三）应用：如图，抛物线y＝ax2＋bx＋c对称轴为直线x=1,交x轴于A、B两点,且点B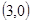
，交y轴于C
点。
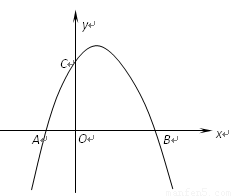
⑴求抛物线的函数关系式；
⑵将△AOC沿x轴翻折得到△AOC′，问：是否存在这样的点P，以P为旋转中心，将△AOC′ 旋转180°，使得A、C′的对称点E、G恰好在抛物线上？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
