
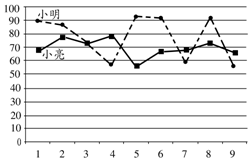
 С����С������ŶӲμ�ij��ѧ�������ñ����Ĺ����ǣ�ÿ�ֱ���һ��ѡ�ֲμӣ�����һ�ֱ����÷���60����һ��ѡ�ֽ����ڶ��֣��ڶ��ֱ����÷���ߵ�ѡ�������Ŷ�ȡ��ʤ����Ϊ���ڱ�����ȡ�ø��õijɼ�����������ǰ�ֱ����˾Ŵβ��ԣ���ͼΪ���˲��Գɼ�����ͳ��ͼ������˵���������ǣ�������
С����С������ŶӲμ�ij��ѧ�������ñ����Ĺ����ǣ�ÿ�ֱ���һ��ѡ�ֲμӣ�����һ�ֱ����÷���60����һ��ѡ�ֽ����ڶ��֣��ڶ��ֱ����÷���ߵ�ѡ�������Ŷ�ȡ��ʤ����Ϊ���ڱ�����ȡ�ø��õijɼ�����������ǰ�ֱ����˾Ŵβ��ԣ���ͼΪ���˲��Գɼ�����ͳ��ͼ������˵���������ǣ�������| A�� | �٢� | B�� | �٢� | C�� | �ڢ� | D�� | �ڢ� |
���� �������ͳ��ͼ������������һ������ɣ�
��� �⣺��������ͳ��ͼ֪С���ijɼ���5�θ���С���ijɼ�����1�κ�С����ȣ���С���IJ��Գɼ���ƽ������С���ĸߣ��ʢٴ���
��������ͳ��ͼ֪С�����Գɼ�����С����С�����Գɼ���С�����ȶ����ʢ���ȷ��
�ۡ�С�����Գɼ�����λ����Լ��69��С�����Գɼ�����λ����Լ��90���ʢ۴���
�ܡ�С�����Գɼ���С�����ȶ���С���IJ��Գɼ���С���ߣ�
��С���μӵ�һ�ֱ�����С���μӵڶ��ֱ������ȽϺ������ʢ���ȷ��
��ѡD��
���� ���⿼����ƽ�����ͷ����Լ�������ͼ������������ͳ��ͼ��ȡ��Ϣ��������


 ��У���˿��ֿ���ϵ�д�
��У���˿��ֿ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
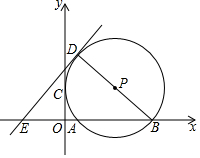 ��ͼ����֪��P��x�ύ��A��B��9��0�����㣬��y����������������C��0��3��������P��ֱ��BD������D��ֱ��DE��BD����x����E�㣬����P��˫����y=$\frac{15}{x}$�ϣ���ֱ��DE�Ľ���ʽΪy=$\frac{12}{7}$x+$\frac{30}{7}$��
��ͼ����֪��P��x�ύ��A��B��9��0�����㣬��y����������������C��0��3��������P��ֱ��BD������D��ֱ��DE��BD����x����E�㣬����P��˫����y=$\frac{15}{x}$�ϣ���ֱ��DE�Ľ���ʽΪy=$\frac{12}{7}$x+$\frac{30}{7}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
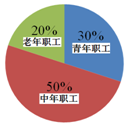 ij��λ��ְ��200�ˣ���������ְ����20-35�꣩������ְ����35-50�꣩������ְ����50�꼰���ϣ���ռ����������ͳ��ͼ��ʾ��
ij��λ��ְ��200�ˣ���������ְ����20-35�꣩������ְ����35-50�꣩������ְ����50�꼰���ϣ���ռ����������ͳ��ͼ��ʾ��| ���� | 26 | 42 | 57 |
| ����ָ�� | 97 | 79 | 72 |
| ���� | 23 | 25 | 26 | 32 | 33 | 37 | 39 | 42 | 48 | 52 |
| ����ָ�� | 93 | 89 | 90 | 83 | 79 | 75 | 80 | 69 | 68 | 60 |
| ���� | 22 | 29 | 31 | 36 | 39 | 40 | 43 | 46 | 51 | 55 |
| ����ָ�� | 94 | 90 | 88 | 85 | 82 | 78 | 72 | 76 | 62 | 60 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
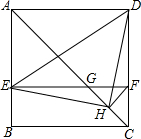 ��ͼ����������ABCD�У�ACΪ�Խ��ߣ�EΪAB��һ�㣬����E��EF��AD����AC��DC�ֱ��ڵ�G��F��HΪCG���е㣬����DE��EH��DH��FH�����н��ۣ�
��ͼ����������ABCD�У�ACΪ�Խ��ߣ�EΪAB��һ�㣬����E��EF��AD����AC��DC�ֱ��ڵ�G��F��HΪCG���е㣬����DE��EH��DH��FH�����н��ۣ��鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com