
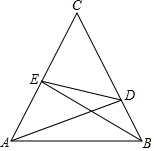
 如图,在△ABC中,AD、BE分别是BC、AC上的高.
如图,在△ABC中,AD、BE分别是BC、AC上的高.分析 (1)首先由在△ABC中,AD、BE分别是BC、AC边上的高,证得△CDA∽△CEB,由相似三角形的对应边成比例即可得出结论;
(2)根据(1)中CDA∽△CEB可得出$\frac{CD}{CA}$=$\frac{CE}{CB}$,进而可得出结论.
解答 (1)证明:∵在△ABC中,AD、BE分别是BC、AC边上的高,
∴∠ADC=∠BEC=90°,
∵∠C是公共角,
∴△CDA∽△CEB,
∴$\frac{CD}{CE}$=$\frac{AC}{BC}$,即CD•BC=CE•AC;
(2)解:△CDE∽△CAB.
∵CDA∽△CEB,∠C是公共角,
∴$\frac{CD}{CA}$=$\frac{CE}{CB}$,
∴△CDE∽△CAB.
点评 本题考查的是相似三角形的判定,熟知两组对应边的比相等且夹角对应相等的两个三角形相似是解答此题的关键.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:选择题
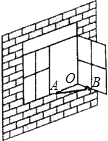 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )| A. | 三角形的稳定性 | B. | 两点之间线段最短 | ||
| C. | N点确定一条直线 | D. | 垂线段最短 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 简单几何体 |  | 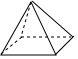 |  | 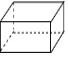 |
| 顶点数(x) | 4 | 5 | 6 | 8 |
| 面数(y) | 4 | 5 | 5 | 6 |
| 棱数(z) | 6 | 8 | 9 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com