
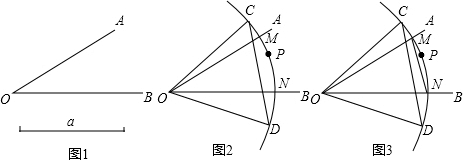
分析 (1)如图2,连结OP,由题意可得$\widehat{MC}$=$\widehat{MP}$,$\widehat{PN}$=$\widehat{DN}$,于是得到∠COM=∠POM,∠PON=∠DON,由已知条件得到∠COD=2∠MON=60°,于是得到结论;
(2)根据他在他家得到∠CON=45°,得到∠OEC=75°,根据等腰三角形的性质得到∠ONM=∠OMN=75°,求得∠OEC=∠ONM,根据平行线的判定定理即可得到结论;
(3)当P是$\widehat{MN}$的中点时,MN∥CD;根据题意作出图形即可.
解答 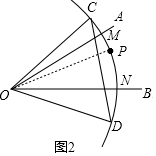 解:(1)如图2,连结OP,
解:(1)如图2,连结OP,
由题意可得$\widehat{MC}$=$\widehat{MP}$,
∴∠COM=∠POM,$\widehat{PN}$=$\widehat{DN}$,
∴∠PON=∠DON,
∴∠POM+∠PON=∠COM+∠DON=30°,
∴∠COD=2∠MON=60°,
∴△OCD是等边三角形;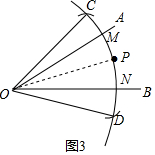
(2)不一定,只有当∠COM=15°,CD∥MN,
理由:∵∠COM=15°,∠MON=30°,
∴∠CON=45°,
∵∠C=60°,
∴∠OEC=75°,
∵ON=OM,
∴∠ONM=∠OMN=75°,
∴∠OEC=∠ONM,
∴CD∥MN;
(3)当P是$\widehat{MN}$的中点时,MN∥CD;如图3所示.
点评 本题考查了作图-复杂作图,平行线的判定和性质,等边三角形的性质,正确的作出图形是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:解答题
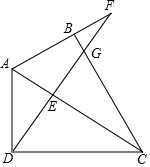 如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.
如图,在四边形ABCD中,∠ABC=∠ADC=90°,DF⊥AC于E,且与AB的延长线相交于F,于BC相交于G,求证:AD2=AB•AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
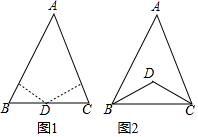 已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.
已知:点D到△ABC的两边AB、AC所在直线的距离相等,且DB=DC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
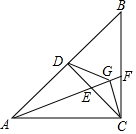 如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.
如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com