练习册

  • 练习册
  • 试题
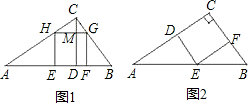    精英家教网 > 初中数学 > 题目详情
    精英家教网如图是一块直角三角形木板，∠C=90°，AB=5cm，AC=4cm，现要把它加工成一个正方形，请你设计一个方案，怎样裁才能使正方形的面积最大？并求出这个最大正方形的边长．
    分析：首先根据勾股定理求得BC的长，然后分别求得正方形的其中两条边在直角三角形的两条直角边上的正方形的面积和以正方形的一边在直角三角形的斜边上的正方形的面积，再进一步比较它们的大小即可．
    解答：精英家教网解：BC=
    		AB2-AC2
    =
    		52-42
    =3    ．
    设正方形的边长为xcm，
    方案①，如图1，正方形EFGH为设计正方形，
    因为HG∥AB，
    所以
    HG
    AB
    =
    CM
    CD
    ，
    又CD=
    12
    5
    ，CM=
    12
    5
    -x    ，
    则
    x
    5
    =
    12
    5
    -x
    12
    5
    ，
    解x=
    60
    37
    ；
    方案②，如图2，正方形CDEF为设计正方形，
    因为DE∥BC，
    所以
    DE
    BC
    =
    AD
    AC
    ，
    即
    x
    3
    =
    4-x
    4
    ，
    解得x=
    12
    7
    ，
    因为
    60
    37
    ＜
    12
    7
    ，
    所以根据方案②的设计可得面积最大正方形，这时边长为
    12
    7
    ．
    点评：此题综合运用了勾股定理以及相似三角形的判定及性质．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    28、操作与探究：
    （1）图①是一块直角三角形纸片．将该三角形纸片按如图方法折叠，是点A与点C重合，DE为折痕．试证明△CBE等腰三角形；
    （2）再将图①中的△CBE沿对称轴EF折叠（如图②）．通过折叠，原三角形恰好折成两个重合的矩形，其中一个是内接矩形，另一个是拼合（指无缝无重叠）所成的矩形，我们称这样的两个矩形为“组合矩形”．你能将图③中的△ABC折叠成一个组合矩形吗？如果能折成，请在图③中画出折痕；
    （3）请你在图④的方格纸中画出一个斜三角形，同时满足下列条件：①折成的组合矩形为正方形；②顶点都在格点（各小正方形的顶点）上；
    （4）有一些特殊的四边形，如菱形，通过折叠也能折成组合矩形（其中的内接矩形的四个顶点分别在原四边形的四条边上）．请你进一步探究，一个非特殊的四边形（指除平行四边形、梯形外的四边形）满足何条件时，一定能折成组合矩形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，一块直角三角形木板△ABC，将其在水平面上沿斜边AB所在直线按顺时针方向翻滚，使它滚动到△A″B″C″的位置，若BC=1cm，AC=
    		3
    cm，则顶点A运动到A″时，点A所经过的路径是
     
    cm．精英家教网

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年黑龙江伊春区九年级上学期期末检测数学试卷（解析版） 题型：填空题

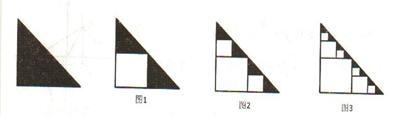
    如图,是一块直角边长为2cm的等腰直角三角形的硬纸板,在期内部裁剪下一个如图1所示的正方形,设得到的剩余部分的面积为；再分别从剩下的两个三角形内用同样的方式裁剪下两个正方形,如图2所示,设所得到的剩余部分的面积为；再分别从剩余的四个三角形内用同样的方式裁剪下四个正方形,如图3所示,设所得到的剩余部分的面积为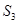；.........,如此下去,第n个裁剪后得到的剩余部分面积=        ．

     

     

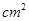    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    如图是一块直角三角形木板，∠C=90°，AB=5cm，AC=4cm，现要把它加工成一个正方形，请你设计一个方案，怎样裁才能使正方形的面积最大？并求出这个最大正方形的边长．

    查看答案和解析>>

    同步练习册答案