
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
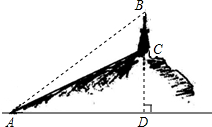 如图,要测量小山上电视塔BC的高度,在山脚下点A测得:塔顶B的仰角为∠BAD=40°,塔底C的仰角为∠CAD=30°,AC=200米,求电视塔BC的高.(结果用含非特殊角的锐角三角函数及根式表示即可)
如图,要测量小山上电视塔BC的高度,在山脚下点A测得:塔顶B的仰角为∠BAD=40°,塔底C的仰角为∠CAD=30°,AC=200米,求电视塔BC的高.(结果用含非特殊角的锐角三角函数及根式表示即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
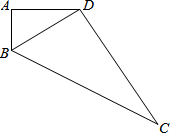 已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.
已知,如图,∠A=90°,AB=3,AD=4,CD=12,BC=13.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com