
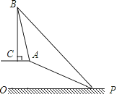
【题目】已知,如图,在笔山银子岩坡顶![]() 处的同一水平面上有一座移动信号发射塔
处的同一水平面上有一座移动信号发射塔![]() ,
,
笔山职中数学兴趣小组的同学在斜坡底![]() 处测得该塔的塔顶
处测得该塔的塔顶![]() 的仰角为
的仰角为![]() ,然后他们沿着坡度为
,然后他们沿着坡度为![]() 的斜坡
的斜坡![]() 攀行了
攀行了![]() 米,在坡顶
米,在坡顶![]() 处又测得该塔的塔顶
处又测得该塔的塔顶![]() 的仰角为
的仰角为![]() .求:
.求:
![]() 坡顶
坡顶![]() 到地面
到地面![]() 的距离;
的距离;
![]() 移动信号发射塔
移动信号发射塔![]() 的高度(结果精确到
的高度(结果精确到![]() 米).
米).
(参考数据:![]() ,
,![]() ,
,![]() )
)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校随机抽查了部分九年级女生进行1分钟仰卧起坐测试,并将测试的结果绘制成了如图的不完整的统计表和频数分布直方图(注:在频数分布直方图中,每组含左端点,但不含右端点):
仰卧起坐次数的范围(次) | 15~20 | 20~25 | 25~30 | 30~35 |
频数 | 3 | 10 | 12 |
|
频率 |
|
|
|
|

(1)30~35的频数是 、25~30的频率是 .并把统计图补充完整;
(2)被抽查的所有女同学仰卧起坐次数的中位数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
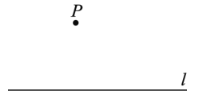
【题目】下面是小东设计的“过直线外一点作这条直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线![]() ,使得
,使得![]() .
.
作法:如图,
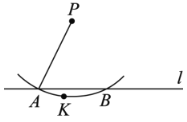
①任意取一点K,使点K和点P在直线l的两旁;
②以P为圆心,![]() 长为半径画弧,交l于点
长为半径画弧,交l于点![]() ,连接
,连接![]() ;
;
③分别以点![]() 为圆心,以
为圆心,以![]() 长为半径画弧,两弧相交于点Q(点Q和点A在直线
长为半径画弧,两弧相交于点Q(点Q和点A在直线![]() 的两旁);
的两旁);
④作直线![]() .
.
所以直线![]() 就是所求作的直线.
就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接![]() ,
,
![]() ______,
______,![]() ______,
______,
![]() 四边形
四边形![]() 是平行四边形(__________)(填推理依据).
是平行四边形(__________)(填推理依据).
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
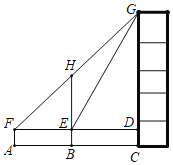
【题目】如图,某数学兴趣小组为测量一颗古树![]() 和教学楼
和教学楼![]() 的高,先在处用高15米的测角仪
的高,先在处用高15米的测角仪![]() 测得古树顶端
测得古树顶端![]() 的仰角
的仰角![]() 为45°,此时教学楼顶端
为45°,此时教学楼顶端![]() 恰好在视线
恰好在视线![]() 上,再向前走10米到达
上,再向前走10米到达![]() 处,又测得教学楼顶端
处,又测得教学楼顶端![]() 的仰角
的仰角![]() 为60°,点
为60°,点![]() 、
、![]() 、
、![]() 三点在同一水平线上.
三点在同一水平线上.
(1)求古树![]() 的高;
的高;
(2)求教学楼![]() 的高.(参考数据:
的高.(参考数据:![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E为BC边的中点,把△ABE沿直线AE折叠,B点落在点B′处,B′B与AE交于点F,连接AB′,DB′,FC.下列结论:①AB′=AD;②△FCB′为等腰直角三角形;③∠CB′D=135°;④BB′=BC;⑤![]() .其中正确的个数为( ).
.其中正确的个数为( ).
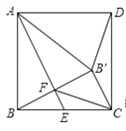
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在标有平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形的六张形状、大小完全相等的纸片中,连续抽取其中两张纸片,被抽中的(所对应的图形)恰好是轴对称的概率是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上(不与
上(不与![]() 重合),将矩形沿
重合),将矩形沿![]() 折叠,使点
折叠,使点![]() 分别落在点
分别落在点![]() 处有下列结论:
处有下列结论:
①![]() 与
与![]() 互余;
互余;
②若![]() 平分
平分![]() 则
则![]()
③若直线![]() 经过点
经过点![]() 则
则![]()
④若直线![]() 交边
交边![]()
![]() 分别于
分别于![]() 当
当![]() 为等腰三角形时,五边形
为等腰三角形时,五边形![]() 的周长为
的周长为![]() .其中正确结论的序号是_____________________.
.其中正确结论的序号是_____________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
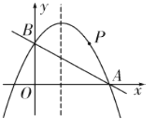
(1)求抛物线的解析式;
(2)若![]() 是抛物线上一点,且
是抛物线上一点,且![]() 点坐标为
点坐标为![]() ,点
,点![]() 为抛物线对称轴上一点,求
为抛物线对称轴上一点,求![]() 的最小值;
的最小值;
(3)点![]() 为直线
为直线![]() 上的动点,点
上的动点,点![]() 为抛物线上的动点,当以点
为抛物线上的动点,当以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形时,求点
为顶点的四边形是平行四边形时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com