
分析 (1)先去分母,再去括号得到3x-6≤14-2x,接着移项、合并得5x≤20,然后把x的系数化为1得到不等式的解集,再写出解集中的正整数即可;
(2)分别解两不等式得到x≤4和x>2,然后根据大小小大中间找确定不等式组的解集.
解答 解:(1)去分母得3(x-2)≤2(7-x),
去括号得3x-6≤14-2x,
移项得3x+2x≤14+6,
合并得5x≤20,
系数化为1得x≤4,
所以不等式的正整数解为1、2、3、4;
(2)$\left\{\begin{array}{l}{3x+2≤2(x+3)①}\\{\frac{2x-1}{3}>\frac{x}{2}②}\end{array}\right.$,
解①得x≤4,
解②得x>2,
所以不等式组的解集为2<x≤4.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.也考查了解一元一次不等式.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
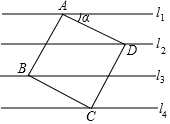 如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )
如图,已知直线l1∥l2∥l3∥l4,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则sinα=( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=1,b=-3,c=-1 | B. | a=1,b=-3,c=1 | C. | a=-1,b=-3,c=1 | D. | a=-1,b=3,c=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com