
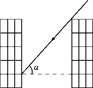
【题目】小明家在某小区买了一套住房,该小区楼房均为平顶式,南北朝向,楼高统一为16米(五层),小明在冬至正午测得南楼落在北楼上的影子有3.5米高(如图),且已知两楼相距有20米,请你帮小明求此时太阳光与水平线的夹角α的度数(结果精确到1°).
【答案】32°.
【解析】
试题过点C作CE⊥AB于点E,则CD=BE=3.5米,CE=BD=20米,AB=16米,进而可求得AE的长,在Rt△ACE中,结合三角函数的知识即可求出∠ACE的度数,注意结果要精确到0.1°.
试题解析:根据题意画出示意图,如图所示.
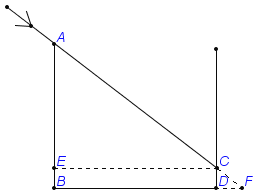
过点C作CE⊥AB于点E,则CD=BE=3.5米,CE=BD=20米,AB=16米.
∵ AB=16米 BE=3.5米
∴ AE=AB-BE=12.5(米)
∵ 在Rt△ACE中,AE=12.5米,CE=20米
∴tan∠ACE=![]() =0.625(三角函数定义)
=0.625(三角函数定义)
∴ ∠α≈32.0°
即冬至这天该市在正午时分太阳光线与水平线的夹角大小约为32.0°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
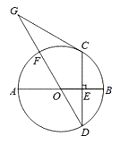
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知BC=6,BC边上中线AD=5.点P为线段AD上一点(与点A、D不重合),过P点作EF∥BC,分别交边AB、AC于点E、F,过点E、F分别作EG∥AD,FH∥AD,交BC边于点G、H.
(1)求证:P是线段EF的中点;
(2)当四边形EGHF为菱形时,求EF的长;
(3) 如果sin∠ADC=![]() ,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c–3b<0;⑤a+b>n(an+b)(n≠1),其中正确的结论有( )
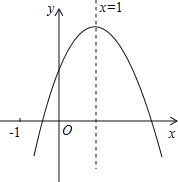
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD外取一点E,连接AE、BE、DE.过点A作AE的垂线交DE于点P.若AE=AP=1,PB=![]() .下列结论:①△APD≌△AEB;②点B到直线AE的距离为
.下列结论:①△APD≌△AEB;②点B到直线AE的距离为![]() ;③EB⊥ED;④S△APD+S△APB=1+
;③EB⊥ED;④S△APD+S△APB=1+![]() ;⑤S正方形ABCD=4+
;⑤S正方形ABCD=4+![]() .其中正确结论的序号是( )
.其中正确结论的序号是( )

A.①③④ B.①②⑤ C.③④⑤ D.①③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
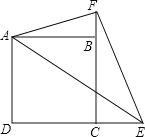
【题目】正方形ABCD中,点E在DC延长线上,点F在CB延长线上,∠EAF=45°,∠BAF=15°
(1)求证:DE﹣EF=BF;
(2)若AD=![]() ,求△AEF的面积.
,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个口袋中有9个红球和若干个白球,在不允许将球倒出来数的前提下,小明采用如下的方法估算其中白球的个数:从口袋中随机摸出一球,记下颜色,然后把它放回口袋中,摇匀后再随机摸出一球,记下颜色…,小明重复上述过程共摸了100次,其中40次摸到白球,请回答:
(1)口袋中的白球约有多少个?
(2)有一个游乐场,要按照上述红球、白球的比例配置彩球池,若彩球池里共有1200个球,则需准备多少个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 A、B是线段MN上的两点,MN4,MA1,MB1.以A为中心顺 时针旋转点M,以B为中心逆时针旋转点N,使MN 两点重合成一点C,构成△ABC,设ABx.(1)则x的取值范围是_________;(2)△ABC的最大面积是_________.
C 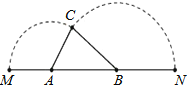
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com