
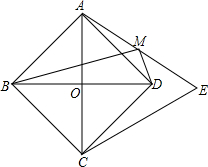
 如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM.
如图所示,在正方形ABCD中,对角线AC,BD交于点O,以AC为边作等边△ACE,M为AE的中点.求证:BM⊥DM. 分析 连接OM、DE,先证明O、D、E在一条直线上,再证明OA=OM=AM=OD=OB,证出∠AOM=60°,∠DOM=30°,得出∠OMB=15°,∠OMD=75°,证出∠BMD=90°,即可得出结论.
解答 证明:连接OM、DE,如图所示: ∵四边形ABCD是正方形,△ACE是等边三角形,
∵四边形ABCD是正方形,△ACE是等边三角形,
∴AD=CD,OA=$\frac{1}{2}$AC,OB=$\frac{1}{2}$BD,AC⊥BD,AC=AE=CE,
∴∠AOD=90°,D、E都在AC的垂直平分线上,
∴O、D、E在一条直线上,
∵M是AE的中点,
∴OM=$\frac{1}{2}$AE=AM,
∴OA=OM=AM=OD=OB,
∴∠AOM=60°,
∴∠DOM=30°,
∴∠OMB=15°,∠OMD=75°,
∴∠BMD=90°,
∴BM⊥DM.
点评 本题考查了正方形的性质、等边三角形的判定与性质、直角三角形的中线性质;证明三点共线和等边三角形是解决问题的关键.


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
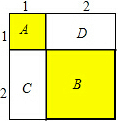 我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
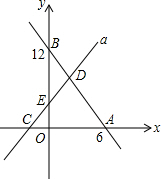 如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.
如图,直线m为y=x+3,且直线a与x轴交于点C,直线b经过A、B两点,两直线相交于点D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
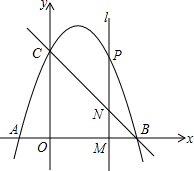 如图,直线BC交x轴、y轴于点B(3,0)和C(0,3),且抛物线y=-x2+bx+c过B、C两点,与x轴交于另一点A.
如图,直线BC交x轴、y轴于点B(3,0)和C(0,3),且抛物线y=-x2+bx+c过B、C两点,与x轴交于另一点A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com