
【题目】如图,△ABC,△ADE是等边三角形,B,C,D在同一直线上.
求证:(1)CE=AC+CD;(2)∠ECD=60°.

【答案】证明见解析
【解析】
(1)根据△ABC、△ADE都是等边三角形,得到AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,推出∠BAD=∠CAE,得到△BAD≌△CAE,根据全等三角形的性质得到BD=EC,即可推出答案;
(2)由(1)知:△BAD≌△CAE,根据平角的意义即可求出∠ECD的度数.
(1)∵△ABC,△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,∴△BAD≌△CAE(SAS),
∴BD=EC.∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD.
(2)由(1)知△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°-∠ACB-∠ACE=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,双曲线![]() 和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
和直线y=kx+b交于A,B两点,点A的坐标为(﹣3,2),BC⊥y轴于点C,且OC=6BC.
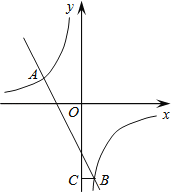
(1)求双曲线和直线的解析式;
(2)直接写出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是_____.
①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是矩形ABCD的对角线,过AC的中点O作EF⊥AC,交BC于点E,交AD于点F,连接AE,CF.
(1)求证:四边形AECF是菱形;
(2)若AB=![]() ,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
,∠DCF=30°,求四边形AECF的面积.(结果保留根号)
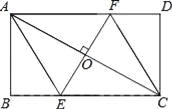
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).
(1)请在如图所示的网格平面内作出平面直角坐标系;
(2)请作出△ABC关于y轴对称的△A1B1C1;
(3)写出点B1的坐标;
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解下列各题:
(1)先化简,再求代数式(![]() 的值,其中x=
的值,其中x=![]() cos30°+
cos30°+![]() ;
;
(2)已知α是锐角,且sin(α+15°)=![]() .计算
.计算![]() -4cosα-(π-3.14)0+tanα+(
-4cosα-(π-3.14)0+tanα+(![]() )-1的值.
)-1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
小明遇到一个问题:在![]() 中,
中,![]() ,
,![]() ,
,![]() 三边的长分别为
三边的长分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的面积.
的面积.
小明是这样解决问题的:如图①所示,先画一个正方形网格(每个小正方形的边长为![]() ),再在网格中画出格点
),再在网格中画出格点![]() (即
(即![]() 三个顶点都在小正方形的顶点处),从而借助网格就能计算出
三个顶点都在小正方形的顶点处),从而借助网格就能计算出![]() 的面积.他把这种解决问题的方法称为构图法.
的面积.他把这种解决问题的方法称为构图法.
参考小明解决问题的方法,完成下列问题:
(![]() )图
)图![]() 是一个
是一个![]() 的正方形网格(每个小正方形的边长为
的正方形网格(每个小正方形的边长为![]() ) .
) .
①利用构图法在答卷的图![]() 中画出三边长分别为
中画出三边长分别为![]() 、
、![]() 、
、![]() 的格点
的格点![]() .
.
②计算①中![]() 的面积为__________.(直接写出答案)
的面积为__________.(直接写出答案)
(![]() )如图
)如图![]() ,已知
,已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,
,![]() ,连接
,连接![]() .
.
①判断![]() 与
与![]() 面积之间的关系,并说明理由.
面积之间的关系,并说明理由.
②若![]() ,
,![]() ,
,![]() ,直接写出六边形
,直接写出六边形![]() 的面积为__________.
的面积为__________.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com