
【题目】关于x的二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.
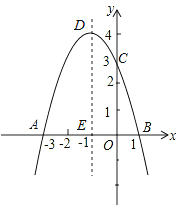
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1) y=-x2-2x+3,(2)存在;(-1,![]() -1)或(-1,-
-1)或(-1,-![]() -1).
-1).
【解析】
试题(1)把A、C两点坐标代入可求得b、c,可求得抛物线解析式;
(2)当点P在∠DAB的平分线上时,过P作PM⊥AD,设出P点坐标,可表示出PM、PE,由角平分线的性质可得到PM=PE,可求得P点坐标;当点P在∠DAB外角平分线上时,同理可求得P点坐标.
试题解析:(1)∵二次函数y=-x2+bx+c经过点A(-3,0),点C(0,3),
∴![]() ,
,
解得![]() ,
,
∴抛物线的解析式y=-x2-2x+3,
(2)存在,
当P在∠DAB的平分线上时,如图1,作PM⊥AD,
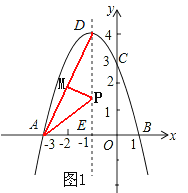
设P(-1,m),则PM=PDsin∠ADE=![]() (4-m),PE=m,
(4-m),PE=m,
∵PM=PE,
∴![]() (4-m)=m,m=
(4-m)=m,m=![]() -1,
-1,
∴P点坐标为(-1,![]() -1);
-1);
当P在∠DAB的外角平分线上时,如图2,作PN⊥AD,
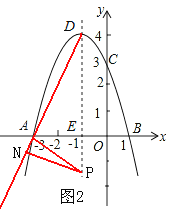
设P(-1,n),则PN=PDsin∠ADE=![]() (4-n),PE=-n,
(4-n),PE=-n,
∵PN=PE,
∴![]() (4-n)=-n,n=-
(4-n)=-n,n=-![]() -1,
-1,
∴P点坐标为(-1,-![]() -1);
-1);
综上可知存在满足条件的P点,其坐标为(-1,![]() -1)或(-1,-
-1)或(-1,-![]() -1).
-1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
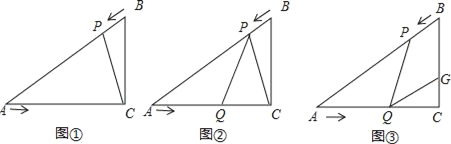
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 y=ax2+bx+c 的图象与 x 轴的交点的横坐标分别为-1,3,则:
①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意 x 均有 ax2+bx≥a+b,其中结论正确的个数有( )
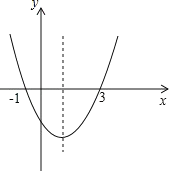
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
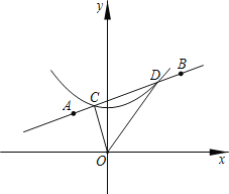
【题目】如图,在平面直接坐标系中,将反比例函数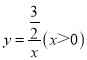 的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点
的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点![]() ,
,![]()
![]() 的直线与曲线l相交于点C、D,则sin∠COD=___ .
的直线与曲线l相交于点C、D,则sin∠COD=___ .
查看答案和解析>>
科目:初中数学 来源: 题型:
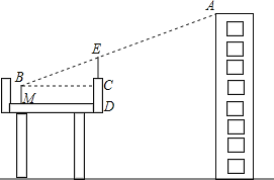
【题目】为了减轻二环高架上汽车的噪音污染,成都市政府计划在高架上的一些路段的护栏上方增加隔音屏.如图,工程人员在高架上的车道M处测得某居民楼顶的仰角∠ABC的度数是20°,仪器BM的高是0.8m,点M到护栏的距离MD的长为11m,求需要安装的隔音屏的顶部到桥面的距离ED的长(结果保留到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
查看答案和解析>>
科目:初中数学 来源: 题型:
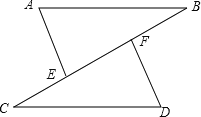
【题目】如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.
(1)求证:BE=CF.
(2)若AB=CF,∠B=40°,求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
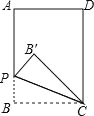
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=__________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com