
【题目】如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
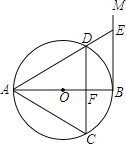
(1)求证:△ACD是等边三角形.
(2)连接OE,若DE=2,求OE的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
试题分析:(1)由AB是⊙O的直径,BM是⊙O的切线,得到AB⊥BE,由于CD∥BE,得到CD⊥AB,根据垂径定理得到![]() =
=![]() ,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
,于是得到AD=AC,然后根据已知DA=DC,得出AD=AC=CD,即可证得;
(2)连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,得到∠DAC=60°又直角三角形的性质得到BE=![]() AE,ON=
AE,ON=![]() AO,设⊙O的半径为:r则ON=
AO,设⊙O的半径为:r则ON=![]() r,AN=DN=
r,AN=DN=![]() r,由于得到EN=2+
r,由于得到EN=2+![]() r,BE=AE=
r,BE=AE=![]() ,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
,在Rt△DEF与Rt△BEO中,由勾股定理列方程即可得到结论.
(1)证明:∵AB是⊙O的直径,BM是⊙O的切线,
∴AB⊥BE,
∵CD∥BE,
∴AB⊥CD,
∴![]() =
=![]() ,
,
∴AD=AC,
∵DA=DC,
∴AD=AC=CD,
∴△ACD是等边三角形;
(2)解:连接OE,过O作ON⊥AD于N,由(1)知,△ACD是等边三角形,
∴∠DAC=60°
∵AD=AC,CD⊥AB,
∴∠DAB=30°,
∴BE=![]() AE,ON=
AE,ON=![]() AO,
AO,
设⊙O的半径为:r,
∴ON=![]() r,AN=DN=
r,AN=DN=![]() r,
r,
∴EN=2+![]() r,BE=
r,BE=![]() AE=
AE=![]() ,
,
在Rt△NEO与Rt△BEO中,
OE2=ON2+NE2=OB2+BE2,
即(![]() )2+(2+
)2+(2+![]() )2=r2+(
)2=r2+(![]() )2,
)2,
∴r=2![]() ,
,
∴OE2=(![]() )2+25=28,
)2+25=28,
∴OE=2![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
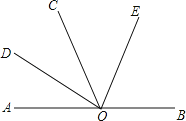
(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上,则a的值是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F分别是平行四边形ABCD的边AB,DC上的点,AF与DE相交于点P,FB与EC相交于点B,若S△APD=15cm2,S△BQC=25cm2,则阴影部分的面积为( )
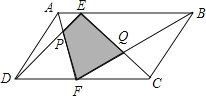
A.10cm2 B.20cm2 C.30cm2 D.40cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在红城中学举行的“我爱祖国”征文活动中,七年级和八年级共收到征文118篇,且七年级收到的征文篇数是八年级收到的征文篇数的一半还少2篇,求七年级收到的征文有多少篇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:数轴上A、B两点表示的有理数分别为a、b,且(a﹣1)2+|b+2|=0,
(1)求(a+b)2015的值.
(2)数轴上的点C与A、B两点的距离的和为7,求点C在数轴上表示的数c的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com