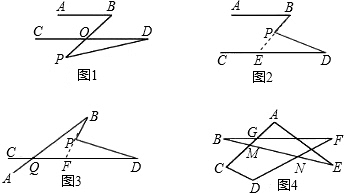
解:(1)不成立,∠BPD=∠B+∠D,
理由是:延长BP交CD于E,如图2,
∵AB∥CD,
∴∠B=∠BED,
∵∠BPD=∠BED+∠D,
∴∠BPD=∠B+∠D;
(2)如图3,∠BPD=∠B+∠BQD+∠D,
理由是:延长BP交CD于F,
∵∠BFD=∠B+∠BQD,∠BPD=∠BFD+∠D,
∴∠BPD=∠B+∠BQD+∠D;
(3)∵∠CMN=∠A+∠E,∠DNB=∠B+∠F,
又∵∠C+∠D+∠CMN+∠DNM=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
分析:(1)∠BPD=∠B+∠D,延长BP交CD于E,根据平行线性质得出∠B=∠BED,根据三角形外角性质得出∠BPD=∠BED+∠D,代入即可;
(2)∠BPD=∠B+∠BQD+∠D,延长BP交CD于F,根据三角形外角性质得出∠BFD=∠B+∠BQD,∠BPD=∠BFD+∠D,即可得出答案;
(3)根据三角形外角性质得出∠CMN=∠A+∠E,∠DNB=∠B+∠F,代入∠C+∠D+CMN+∠DNM=360°即可求出答案.
点评:本题考查了平行线性质,三角形外角性质,四边形的内角和定理等知识点的应用,主要考查学生的推理能力和猜想能力.

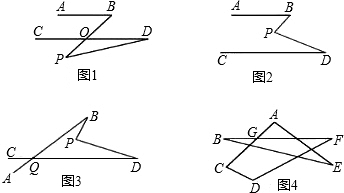
 解:(1)不成立,∠BPD=∠B+∠D,
解:(1)不成立,∠BPD=∠B+∠D,

