

分析 (1)首先过点E分别作BC、CD的垂线,垂足分别为H、P,然后利用ASA证得Rt△FEP≌Rt△GEH,则问题得证;
(2)过点E作EM⊥BC于M,过点E作EN⊥CD于N,垂足分别为M、N,过点C作CP⊥EG交EG的延长线于点P,过点C作CQ⊥EF垂足为Q,可得四边形EPCQ是矩形,四边形EMCN是矩形,可得EC平分∠FEG,可得矩形EPCQ是正方形,然后易证△PCG≌△QCF(AAS),进而可得:CG=CF,由EM∥AB,EN∥AD知△CEN∽△CAD,△CEM∽△CAB,从而可得$\frac{EF}{EG}=\frac{BC}{AB}$=2,进而可得:EF=2EG,然后易证EM和EN分别是△ABC和△BCD的中位线,进而可得:EM=1,EN=2,MC=2,CN=1,然后易证△EMG∽△ENF,进而可得$\frac{MG}{NF}=\frac{EM}{EN}=\frac{1}{2}$,即NF=2MG,然后设MG=x,根据CG=CF,列出方程即可解出x的值,即MG的值,然后在Rt△EMG中,由勾股定理即可求出EG的值,进而可得EF的值.
解答 解:(1)如图1,过点E作EH⊥BC于H,过点E作EP⊥CD于P,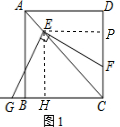
∵四边形ABCD为正方形,
∴CE平分∠BCD,
又∵EH⊥BC,EP⊥CD,
∴EH=EP,
∴四边形EHCP是正方形,
∴∠HEP=90°,
∵∠GEH+∠HEF=90°,∠PEF+∠HEF=90°,
∴∠PEF=∠GEH,
∴Rt△FEP≌Rt△GEH,
∴EF=EG;
(2)如图2,过点E作EM⊥BC于M,过点E作EN⊥CD于N,垂足分别为M、N,
过点C作CP⊥EG交EG的延长线于点P,过点C作CQ⊥EF垂足为Q,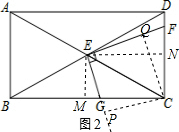
则四边形EPCQ是矩形,四边形EMCN是矩形,
∵EC平分∠FEG,
∴CQ=CP,
∴矩形EPCQ是正方形,
∴∠QCP=90°,
∴∠QCG+∠PCG=90°,
∵∠QCG+∠QCF=90°,
∴∠PCG=∠QCF,
在△PCG和△QCF中,
∵$\left\{\begin{array}{l}{∠PCG=∠QCF}\\{∠CPG=∠CQF=90°}\\{PC=CQ}\end{array}\right.$,
∴△PCG≌△QCF(AAS),
∴CG=CF,
∵EM∥AB,EN∥AD.
∴△CEN∽△CAD,△CEM∽△CAB,
∴$\frac{NE}{AD}=\frac{CE}{CA}$、$\frac{EM}{AM}=\frac{CE}{CA}$,
∴$\frac{NE}{AD}$=$\frac{EM}{AB}$,
即$\frac{EN}{EM}=\frac{AD}{AB}$=$\frac{BC}{AB}$,
∴$\frac{EF}{EG}=\frac{BC}{AB}$,
∵BC=4,AB=2,
∴$\frac{EF}{EG}$=$\frac{BC}{AB}$=2,
∴EF=2EG,
∵点E放在矩形ABCD的对角线交点,
∴EM和EN分别是△ABC和△BCD的中位线,
∴EM=$\frac{1}{2}$AB=1,EN=$\frac{1}{2}$AD=2,MC=$\frac{1}{2}$BC=2,CN=$\frac{1}{2}$CD=1,
∵四边形EMCN是矩形,
∴∠NEM=90°,
∴∠MEG+∠GEN=90°,
∵∠GEF=90°,
∴∠FEN+∠GEN=90°,
∴∠MEG=∠FEN,
∵∠EMG=∠FNE=90°,
∴△EMG∽△ENF,
∴$\frac{MG}{NF}$=$\frac{EM}{EN}$=$\frac{1}{2}$,
即NF=2MG,
设MG=x,则NF=2x,CG=2-x,CF=1+2x,
∵CG=CF,
∴2-x=1+2x,
解得:x=$\frac{1}{3}$,
∴MG=$\frac{1}{3}$,
在Rt△EMG中,由勾股定理得:
EG=$\sqrt{E{M}^{2}+M{G}^{2}}$=$\frac{\sqrt{10}}{3}$,
∵EF=2EG,
∴EF=$\frac{2\sqrt{10}}{3}$.
点评 此题考查了正方形,矩形的性质,以及全等三角形与相似三角形的判定与性质.此题综合性较强,注意数形结合思想的应用.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:选择题
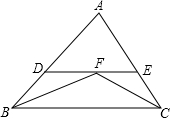 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于点D,交AC于点E.若BD+CE=2013,则线段DE的长为( )| A. | 2014 | B. | 2011 | C. | 2012 | D. | 2013 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 100 | B. | 121 | C. | 181 | D. | 1021 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
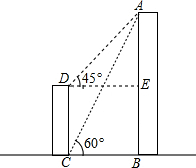 如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,AB、CD为两栋建筑物,建筑物CD的高度为20m,从建筑物CD的顶部D点测得建筑物AB的顶部A点的仰角为45°,从建筑物CD的底部C点测得建筑物AB的顶部A点的仰角60°,求建筑物AB的高度(结果保留整数)(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com