
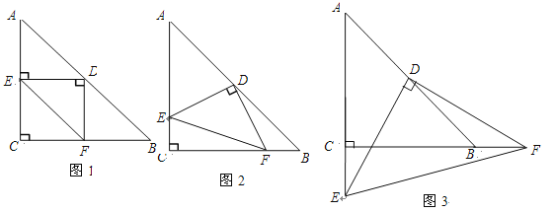
【题目】 已知Rt△ABC中,AC=BC,∠C=90°,D为AB边的中点,∠EDF=90°,∠EDF绕D点旋转,它的两边分别交AC、CB(或它们的延长线)于E、F.当∠EDF绕D点旋转到DE⊥AC于E时(如图1),易证![]() .当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,
.当∠EDF绕D点旋转到DE和AC不垂直时,在图2和图3这两种情况下,上述结论是否成立? 若成立,请给予证明;若不成立,![]() ,
,![]() ,
,![]() 又有怎样的数量关系?请写出你的猜想,不需证明.
又有怎样的数量关系?请写出你的猜想,不需证明.
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(1,6)B(n,﹣2)是一次函数y=kx+b的图象和反比例函数y= ![]() 的图象的两个交点,直线与y轴交于C点.
的图象的两个交点,直线与y轴交于C点. 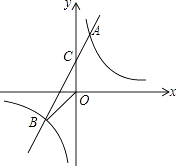
(1)求反比例函数和一次函数的表达式;
(2)求△BOC的面积;
(3)直接写出不等式kx+b﹣ ![]() >0的解集.
>0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
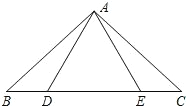
【题目】如图,点 D,E 在△ABC的边 BC上,连接AD,AE.下面有三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成以下三个命题:命题Ⅰ“如果①② 成立,那么③成立”; 命题Ⅱ“如果①③成立,那么②成立”;命题Ⅲ“如果②③成立,那么①成立”.
(1)以上三个命题是真命题的为__________(直接作答);
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小伟和小欣玩一种抽卡片游戏:将背面完全相同、正面分别写有1,2,3,4的四张卡片背面向上洗匀后,小伟和小欣各自随机抽取一张(不放回).将小伟的数字作为十位数字,小欣的数字作为个位数字,组成一个两位数.如果所组成的两位数为偶数,则小伟胜;否则小欣胜.
(1)当小伟抽取的卡片数字为2时,问两人谁获胜的可能性大?
(2)通过计算判断这个游戏对小伟和小欣是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=![]() OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC 的边 AB,AC 向外作等边三角形 ABD 和等边三角形 ACE,线段 BE 与 CD 相交于点 O,连接 OA.
(1)求证:BE=DC;
(2)求∠BOD 的度数;
(3)求证:OA 平分∠DOE.
(4)猜想线段 OA、OB、OD 的数量关系,并证明.
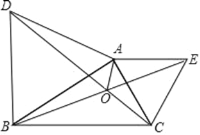
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图①,在△ABC 中,D、E 分别是 AB、AC 上的点,AB=AC,AD=AE,然后将△ADE 绕点 A 顺时针旋转一定角度,连接 BD,CE,得到图②,将 BD、CE 分别延长至 M、N,使 DM=![]() BD,EN=
BD,EN=![]() CE,得到图③,请解答下列问题:
CE,得到图③,请解答下列问题:
(1)在图②中,BD 与 CE 的数量关系是 ;
(2)在图③中,猜想 AM 与 AN 的数量关系,∠MAN 与∠BAC 的数量关系,并证明你的猜想.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一根筷子一端放在水里,一端露出水面,筷子变弯了,它真的弯了吗?其实没有,这是光的折射现象,光从空气中射入水中,光的传播方向发生了改变,图中与∠1是同位角的有____________,与∠2是内错角的有________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级![]() 班数学课外兴趣小组在探究:“
班数学课外兴趣小组在探究:“![]() 边形共有多少条对角线”这一问题时,设计了如下表格:
边形共有多少条对角线”这一问题时,设计了如下表格:
多边形的边数 |
|
|
|
|
| … |
从多边形一个顶点出发可引起的对角线条数 | … | |||||
多边形对角线的总条数 | … |
![]() 探究:假若你是该小组的成员,请把你研究的结果填入上表;
探究:假若你是该小组的成员,请把你研究的结果填入上表;
![]() 猜想:随着边数的增加,多边形对角线的条数会越来越多,从
猜想:随着边数的增加,多边形对角线的条数会越来越多,从![]() 边形的一个顶点出发可引的对角线条数为多少,
边形的一个顶点出发可引的对角线条数为多少,![]() 边形对角线的总条数为多少.
边形对角线的总条数为多少.
![]() 应用:
应用:![]() 个人聚会,每不相邻的人都握一次手,共握多少次手?
个人聚会,每不相邻的人都握一次手,共握多少次手?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com